І. Научное мышление и доказательство
Необходимая для каждой науки связь её истин есть отражение связи реальной, существующей независимо от науки и от мышления. Связь эта — отражение связи вещей, их свойств, их отношений и их законов.
Но связь научных истин в подавляющем большинстве случаев не видна сразу, прямо, непосредственно. Если бы истинность каждого положения науки была очевидна, была видна сразу, из самого этого положения, то наука не нуждалась бы в доказательстве, ибо обоснованность каждой истины обусловливающими её связями вещей усматривалась бы в таком случае непосредственно.
В действительности истинность того или иного научного положения, как правило, не очевидна, не усматривается прямым путём, но выясняется из рассмотрения связей между данной истиной и другими истинами, её обосновывающими. Только очень небольшая часть положений науки принимается в качестве истин без всякого доказательства. Это — так называемые аксиомы, вроде положения о том, что если к равным величинам прибавить равные, то получатся также равные. Да и аксиомы не доказываются вовсе не потому, что все они безусловно очевидны. Аксиомы — не безусловно самоочевидные истины, а положения, принятие которых в систему науки оправдывается всеми результатами, следующими из этого принятия и удостоверяемыми практикой.
Значение недоказываемых истин аксиомы получили только потому, что лежащие в их основе простейшие отношения вещей были испытаны и выяснены всем многотысячелетним развитием практики, опыта.
Но аксиомы составляют в каждой науке, опирающейся на них, только небольшую часть её положений. Все остальные положения выясняются в качестве истин не непосредственно и не отдельно от всех других истин, а путём доказательства, т. е. из необходимой связи, в какой они находятся с другими истинами.
Поэтому доказательство — не второстепенный и не случайный элемент квалифицированного мышления. Доказательство есть жизненный нерв научного мышления, первейшее и необходимейшее условие научности всякого утверждения.
В стремлении науки к доказательности обнаруживается одна из коренных и существеннейших черт научной мысли. Наука и научная мысль не терпят голословности. Научным любое утверждение становится только тогда, когда оно обосновано.
При этом обоснование требуется не только в таких науках, как математика, где всё изложение результатов исследования принимает чётко выраженную форму длинной цепи доказательств. Таким же непременным условием научности доказательство является во всех науках, в том числе и в общественных. В вопросах, затрагивающих коренные жизненные интересы общества, никто не обязан и не склонен принимать голословное утверждение за истину. Здесь недостаточна одна лишь сила личного убеждения.
Убеждение — чрезвычайно важное качество и условие практической и теоретической деятельности. Корифеи науки, корифеи марксизма-ленинизма не только владели истиной, не только возвещали истину. Они были людьми, глубоко и горячо убеждёнными в правоте своего дела, в истинности своего учения. Сила их личного убеждения удваивала силу их действия и их влияния на мысль и поведение людей, к которым они обращались.
Однако сила личного убеждения становится могучим фактором познания лишь при условии, если само убеждение есть уверенность в том, что действительно доказано. Пока убеждение остаётся необоснованным, оно не имеет научного значения. Неотразимую силу придаёт мысли не субъективная уверенность, но убеждение обоснованное.
Поэтому классики марксизма-ленинизма во многих — и притом важнейших — своих работах подчёркивали, что научное значение этих работ состоит не просто в открытии или провозглашении новых истин, а в том, что эти открытия или новые истины были ими доказаны.
Так, в письме к Иосифу Вейдемейеру от 5 марта 1852 г. Маркс, характеризуя собственный вклад в развитие науки, писал: «То, что я сделал нового, состояло в доказательстве следующего: 1) что существование классов связано лишь с определенными историческими фазами развития производства; 2) что классовая борьба необходимо ведет к диктатуре пролетариата; 3) что эта диктатура сама составляет лишь переход к уничтожению всяких классов и к бесклассовому обществу»[1].
В письме к И. И. Скворцову-Степанову от 16 декабря 1909 г. В. И. Ленин разъяснил, что значение его подписанного псевдонимом Ильин исследования «Развитие капитализма в России» заключается в доказательстве того, что аграрная Россия в конце XIX века не только вступила на путь капиталистического развития, но что это вступление бесповоротно определило капиталистическую группировку классов. При этом Ленин особо подчеркнул совершенную необходимость этого доказательства. Оно было необходимо, так как вступление России на путь именно капиталистического развития в то время далеко ещё не было для всех очевидным и многими — в том числе и прежде всего народниками — оспаривалось.
И точно так же значение работы И. В. Сталина «Анархизм или социализм?» состояло не просто в том, что здесь была отвергнута доктрина анархизма, а в том, что эта работа представила неопровержимое доказательство ложности теоретических положений анархизма. И. В. Сталин, подчёркивая необходимость доказательства ложности учения анархистов, писал: «Дело не в том, за кем сегодня идёт большая или меньшая «масса»,— дело в существе учения. Если «учение» анархистов выражает истину, тогда оно, само собой разумеется, обязательно проложит себе дорогу и соберёт вокруг себя массу. Если же оно несостоятельно и построено на ложной основе, оно долго не продержится и повиснет в воздухе. Несостоятельность же анархизма должна быть доказана»[2].
Рассмотренные суждения классиков марксизма-ленинизма характеризуют их оценку роли доказательства в научном мышлении.
Логичность мышления проявляется прежде всего в доказательности, обоснованности. Напротив, первое проявление нелогичности и ненаучности мышления — голословность, необоснованность, пренебрежение к строгим условиям и правилам доказательности.
Для значительной части философов современного капиталистического мира доказательность — отнюдь не необходимое и не важнейшее качество мышления. Философы эти стремятся к пересмотру вопроса о значении доказательности.
Стремление это вполне понятно с классовой точки зрения капиталистов. Реакционные и антинародные взгляды и положения, которые согласуются с их корыстными интересами в вопросах политики, истории, права, экономики, философии, эстетики, таковы, что вообще не могут быть доказаны. Взгляды и положения эти не могут быть доказаны, так как они ложны, находятся в вопиющем противоречии с действительностью. А между тем — с точки зрения интересов класса капиталистов — распространение этих взглядов и положений необходимо и желательно. Взгляды эти пропагандируются всеми средствами буржуазной печати, вдалбливаются в головы учащихся в буржуазной школе.
При этих обстоятельствах невозможность доказательства ложных и потому недоказуемых, но выдаваемых за истину положений требует объяснения.
Таким «объяснением» является пересмотр самого вопроса о ценности и необходимости доказательности для мышления. Многие современные буржуазные философы стремятся развенчать логическое значение доказательности, силятся обосновать ненужность доказательства.
Если сравнить трактовку вопроса о доказательстве в буржуазной философской литературе раннего капитализма с современной трактовкой этого вопроса, то обнаружится глубокое различие. На заре своего развития прогрессивная в то время буржуазная мысль устами одного из великих учёных — Б. Паскаля — провозгласила, что научное мышление требует «никогда не утверждать никакого положения, которое не было бы доказано истинами, уже известными»[3].
Напротив, современная буржуазная философия в полном единомыслии с фашистскими мракобесами считает старомодными педантами тех философов и логиков, которые придают ещё серьёзное значение доказательству. В вопросе о доказательстве прагматизм, например, возвращается вспять — ко взглядам реакционного немецкого идеалиста Шопенгауэра, который утверждал, будто «не доказанные суждения, не их доказательства, а суждения, непосредственно почерпнутые из интуиции и на ней вместо всякого доказательства основанные, — вот что в науке является тем, чем солнце в мироздании»[4].
Устами основоположника американского прагматизма Уильяма Джемса философия эта провозгласила «нерациональность» всей действительности и даже отказалась от логики как от орудия мышления. «Что касается меня,— заявил Джемс,— то я счёл себя в конце концов вынужденным отказаться от логики, отказаться от неё открыто, честно и раз навсегда... Я открыто предпочитаю называть действительность, если и не иррациональной, то, по крайней мере, нерациональной в своей структуре...»[5]
Обнажая воочию маразм современной буржуазной мысли, поход против доказательства и доказательности, затеянный философскими мракобесами и декадентами, только резче оттеняет непреложную ценность доказательства в мышлении, цель которого — не извращение, а утверждение истины. Самым убийственным для отрицателей доказательства и в то же время самым смешным в их действиях фактом является то, что ненужность доказательства они пытаются (разумеется, безуспешно) «доказывать». Всё же — доказывать! Тем самым они на деле признают над собою безусловную власть того самого логического принципа, который они в реакционном «раже» бессмысленно отрицают.
ІІ. Доказательство и умозаключение
Так как доказательность — необходимое условие логичности истинного мышления, то в логике возникает вопрос о том, посредством каких форм мысли осуществляется необходимое требование доказательности.
Такой формой мысли является умозаключение.
Умозаключение, опирающееся на истинные посылки, связь которых отвечает логическим законам мышления, даёт результат не только истинный, но и доказанный в качестве истинного. Результат умозаключения есть не только мысль истинная, не только мысль новая, сравнительно с каждой посылкой, отдельно взятой. Результат этот есть, кроме того, мысль доказанная. Доказательством умозаключение делает необходимая логическая связь между истинными посылками и заключением. И наоборот: логическая несостоятельность вывода с истинными посылками может состоять только в отсутствии необходимой логической связи между посылками и заключением, т. е. в бездоказательности вывода.
Но если форма умозаключения есть форма, посредством которой удовлетворяется требование доказательности, то исчерпываются ли возможными формами умозаключений формы доказательства?
В руководствах по логике умозаключение нередко рассматривают лишь как составную часть доказывания истины, формой же обоснования истины считают не умозаключение, а доказательство. Под доказательством в этом случае понимают более или менее длинное рассуждение, посредством которого истина обосновывается и которое состоит из целой цепи умозаключений.
Это понимание доказательства связывается с попытками отличить умозаключение от доказательства в собственном смысле слова. Но какие основания могут быть указаны для такого различения?
Указывают на то, что посылки доказательства необходимо должны быть истинными, в то время как умозаключение — при условии необходимой логической связи между посылками и заключением — остаётся логически безупречным независимо от того, истинны или ложны его посылки[6].
Соображение это не выдерживает критики. И форма отдельного умозаключения и форма, связывающая ряд умозаключений в доказательство, суть формы мышления, направленного на отыскание истины. Для достижения истинного результата истинными должны быть посылки не только сложной цепи умозаключений, но и каждого отдельного умозаключения. Что же касается того, что необходимая логическая связь между посылками и заключением делает заключение необходимым даже в тех случаях, когда и посылки и само заключение ложны, то это верно и в отношении умозаключения и в отношении доказательства. История науки знает огромное множество доказательств, в своё время считавшихся безупречными, так как посылки, на которые они опирались, принимались за истинные, а результат следовал из посылок с логической необходимостью. Впоследствии эти доказательства оказались несостоятельными, так как выяснилось, что посылки их, принимавшиеся за истинные, в действительности ложны. Так, например, в течение столетий физики объясняли подъём воды в насосе тем, что природа будто бы боится пустоты, принимая это как аксиому. Эта аксиома оказалась просто ошибочным утверждением. Однако логическая связь между этой аксиомой и теми положениями, которые выводились из неё в согласии со всеми законами логики, была такой же необходимой, как логическая связь между посылками и заключением последовательного, хотя и опирающегося на ложные посылки, вывода.
Другим основанием для различения между умозаключением и доказательством считают иногда то, что в умозаключении мысль будто бы обязательно идёт от посылок к новому, ещё не известному результату (заключению); напротив, в доказательстве будто бы исходят непременно из тезиса, истинность которого предполагается уже найденной, и подбирают к этому тезису основания, или посылки, из которых этот тезис может быть выведен по законам необходимой логической связи[7].
Соображение это также не выдерживает критики. Оно неверно как по отношению к умозаключению, так и по отношению к доказательству. По отношению к умозаключению оно неверно, так как во множестве случаев, можно сказать даже в подавляющем большинстве случаев, ход мысли в умозаключении, так же как и в доказательстве, состоит вовсе не в том, что соединяют неизвестно почему и для чего посылки, а затем смотрят, какой неизвестный ещё новый результат получится по законам логики из их случайного соединения. Обычно ход мысли в умозаключении, как и в доказательстве, состоит в том, что, имея основание считать известное положение истинным, задаются вопросом, какие известные уже истины могли бы логически обосновать это положение и превратить его, таким образом, из предположения или догадки в доказанную истину. Новизна мысли, получающейся в заключении вывода, есть новизна не в том — психологическом — смысле, что заключение представляет «неожиданный» результат из «случайно» скомбинированных посылок. Новизна заключения есть новизна логическая и состоит только в том, что заключение не содержится ни в одной из посылок, взятой отдельно, вне того их соединения, которое с логической необходимостью обусловливает заключение. Этой — логической — новизне заключения нисколько не противоречит тот факт, что психологически заключение часто предшествует посылкам, из которых оно выводится. Заключение обычно сначала приходит как догадка, посылки же подбираются как истины, логически обосновывающие эту догадку, превращающие её из догадки в доказанное знание.
С другой стороны, в умозаключении, так же как и в доказательстве, мысль может в известных, сравнительно более редких случаях идти от посылок к обосновываемому ими результату. Существуют случаи, когда задача мысли состоит как раз в том, чтобы, исходя из данных суждений как посылок, выяснить, к какому другому суждению необходимо приведёт согласие с данными суждениями.
И в том и в другом случае — идёт ли мысль от результата к посылкам, логически обосновывающим результат, или, наоборот, от посылок к логически обусловленному ими результату — оба эти хода мысли могут встретиться как в умозаключении, так и в доказательстве.
В качестве третьего основания для отличения умозаключения от доказательства выдвигают сложность доказательства сравнительно с умозаключением. Согласно этому взгляду обоснование истины, состоящее из одного единственного вывода, есть умозаключение, обоснование же истины, состоящее из цепи умозаключений, есть доказательство. Различение это может быть принято, но оно, разумеется, не означает принципиального различия между умозаключением и доказательством как логическими формами мышления. В отношении логической формы умозаключение не отличается от доказательства, а доказательство — от умозаключения. И в умозаключении и в доказательстве имеется логическая связь суждений, в силу которой истинностью данных суждений с логической необходимостью обусловливается истинный и притом новый результат. И умозаключение и доказательство — форма связи суждений, в которой отражаются связи самой действительности.
Есть, однако, важные (но не принципиальные) основания для раздельного рассмотрения этих двух, всё же различных, видов обоснования. Дело в том, что в науках обоснования истины обычно выступают не в простой форме отдельных умозаключений, а в сложной форме более или менее длинной цепи умозаключений. При этом длинные цепи умозаключений, многократно применяемые каждой отдельной наукой и различными науками для обоснования научных истин, в ряде случаев имеют особое построение и повторяются в ряде наук или даже во всех науках независимо от конкретности их содержания. Эти ряды умозаключений, имеющие одинаковое логическое построение и не зависящие от конкретных особенностей рассматриваемых в них предметов, мы и будем называть доказательствами.
ІІІ. Доказательство как предмет логики
Чрезвычайно важное значение доказательства для всякого мышления и в особенности для мышления научного делает эту логическую форму важным предметом изучения логики.
Логика изучает строение доказательства, его составные части, виды доказательства, условия его логической безупречности, условия его логической ошибочности, зависимость доказательства от обосновывающих его законов мышления.
При изучении доказательства, так же как и при изучении других логических форм мысли, логика отвлекается от конкретных особенностей содержания отдельных наук. В различных формах доказательства логика изучает то, что является для них общим, несмотря на те или иные конкретные особенности их частного содержания. Если бы логическая форма доказательства всецело зависела от особенностей предмета каждой отдельной науки, то не могло бы существовать общих для всех наук форм доказательства: система видов доказательства, применяемая одной наукой, была бы совершенно неприменима в другой, и таких систем было бы столько, сколько существует отдельных наук.
В логической литературе были попытки представить дело таким образом. Однако попытки эти были продиктованы логикам их философскими и общественно-политическими взглядами, не имеющими отношения к самой логике. Так, Джон Стюарт Милль утверждал, будто индуктивные методы доказательства, с успехом применяемые в науках о явлениях природы, не могут быть применяемы в науках о явлениях общества. При этом Милль исходил из предвзятой и по существу неверной мысли, будто эксперимент, составляющий одно из важнейших звеньев индуктивного доказательства, неосуществим при исследовании общественных отношений и причинных зависимостей общественной жизни.
Другую попытку противопоставить друг другу доказательства естественных и исторических наук представляет логика неокантианцев (Виндельбанд, Риккерт, Гессен, Ласк и др.). Эти логики исходили из противопоставления обобщающих понятий естественных наук понятиям об индивидуальном, будто бы характеризующим исторические науки. Противопоставление это вело не столько к противопоставлению двух систем доказательства, сколько к отрицанию возможности доказательства законов исторического развития общества.
В обоих указанных случаях — в логике Милля и в логике неокантианцев — теория доказательства извращалась под прямым давлением реакционного классового интереса. И отрицание возможности применения индуктивных доказательств в общественных науках (Милль), и характеристика исторических наук, исключающая возможность применения доказательств (Риккерт), имели действительной основой не столько стремление выяснить логическое своеобразие двух типов наук (на что особенно упирали авторы обеих теорий), сколько стремление доказать, будто в области истории не может осуществиться никакое предвидение, основывающееся на познании законов исторического развития.
В действительности же формы доказательства являются общими для всякого научного мышления независимо от конкретных особенностей данной науки.
В этом отношении формы доказательства не отличаются от других логических форм — суждения, понятия, умозаключения. Подобно тому, как одни и те же формы вывода, например силлогизма, могут применяться и в математике, и в физике, и в истории, так одни и те же формы доказательства могут применяться в самых различных по предмету науках.
Возможность такого их применения обнаруживает — на этот раз на примере доказательства.— что логические формы мысли представляют обобщённые формы, отвлечённые от конкретности мыслимого посредством их содержания.
По этой чрезвычайно важной своей черте логика и в теории доказательства, так же как и в теории всех форм логического мышления, напоминает грамматику и математику. И. В. Сталин в работе «Относительно марксизма в языкознании» показал, что сходство этих наук состоит в том, что они изучают отношения предметов и формы, абстрагированные от всякой конкретности. «Отличительная черта грамматики,— говорит И. В. Сталин,— состоит в том, что она даёт правила об изменении слов, имея в виду не конкретные слова, а вообще слова без какой-либо конкретности; она даёт правила для составления предложений, имея в виду не какие-либо конкретные предложения, скажем, конкретное подлежащее, конкретное сказуемое и т. п., а вообще всякие предложения, безотносительно к конкретной форме того или иного предложения... В этом отношении грамматика напоминает геометрию, которая даёт свои законы, абстрагируясь от конкретных предметов, рассматривая предметы, как тела, лишённые конкретности, и определяя отношения между ними не как конкретные отношения таких-то конкретных предметов, а как отношения тел вообще, лишённые всякой конкретности»[8].
Такое отвлечение грамматики от всякой конкретности слов и форм предложения свидетельствует не о слабости грамматики и не о формализме, а, напротив, об её силе и о существенности её анализа. «Грамматика,— писал И. В. Сталин,— есть результат длительной, абстрагирующей работы человеческого мышления, показатель громадных успехов мышления»[9].
Но совершенно таков же подход к изучению форм доказательства и в логике: она изучает обобщённые формы доказательства. Логика, как и грамматика, представляет собой результат длительной абстрагирующей работы ума.
IV. Строение доказательства
Во всяком доказательстве — безотносительно к тому, что именно в нём доказывается, — всегда имеются: 1) тезис, 2) основания доказательства (аргументы) и 3) способ доказательства (демонстрация).
1. Тезис доказательства
Тезисом называется суждение, или положение, истинность (или ложность) которого выясняется посредством данного доказательства. Доказываемый тезис обычно не имеет очевидности. Так, доказываемое в геометрии положение о том, что площадь круга равняется произведению числа π, выражающего отношение длины окружности круга к длине его диаметра, на квадрат радиуса круга, не есть положение самоочевидное. Истинность его обнаруживается доказательством. И так обстоит дело с громадным большинством доказываемых положений.
Даже в случаях, когда доказываемый тезис представляется очевидным, он всё же обычно доказывается (это особенно относится к математике). Так обстоит дело, например, с положением, что диаметром круг делится на две равные части. То, что мыслится в этом положении, представляется очевидным. Однако в геометрии суждение это, несмотря на явную очевидность утверждаемого в нём, доказывается.
Пример этот — не исключение, а иллюстрация общего правила. Наука стремится доказывать, по возможности, всё, что только может быть доказано, безотносительно к тому, очевидно или неочевидно доказываемое.
Это стремление не оставлять, насколько возможно, ни одного положения недоказанным вытекает, во-первых, из уже выясненного выше значения доказательности для научного мышления. Во-вторых, стремление это обусловлено тем, что очевидность нас иногда обманывает. Так, если мы станем между рельсами на полотне железной дороги и поглядим вдаль, то нам непременно покажется, будто рельсы, параллельные на недалёком от нас расстоянии, вдали от нас сходятся в одной точке. Однако очевидность эта обманчива. В действительности рельсы и вдали от нас остаются параллельными.
Так как очевидность во многих случаях вводит нас в заблуждение, то наука стремится как можно меньше полагаться на одну лишь очевидность. Неочевидное доказывается потому, что оно неочевидно, очевидное проверяется доказательством. Поэтому наука всюду, где это только возможно, не оставляет без доказательства даже таких положений, которые представляются совершенно «наглядными», очевидными.
Выяснение истинности или ложности тезиса есть цель всякого доказательства. Доказательство, посредством которого выясняется истинность тезиса, называется просто доказательством. Доказательство, посредством которого выясняется ложность тезиса, называется опровержением. Опровергнуть некоторый тезис — значит доказать, что он ложен, т. е. не соответствует действительности.
Доказательство, в результате которого истинность доказываемого тезиса (или ложность опровергаемого тезиса) выясняется с полной необходимостью и непреложностью, будет безупречным с логической точки зрения.
Доказательство, не приводящее к этому результату, будет ошибочным, или, по крайней мере, неточным в логическом отношении.
Независимо от степени субъективной уверенности доказывающего в истинности доказываемого конечный успех доказательства возможен лишь в том случае, если доказываемый тезис — безотносительно к тому, что о нём думает сам доказывающий,— истинен по существу своего содержания. Можно успешно доказать истинность лишь того, что действительно истинно. И точно также можно успешно доказать ложность только того, что действительно ложно.
Поэтому первое условие, необходимое для безупречности доказательства, есть истинность тезиса по существу его содержания[10]. Разумеется, истинность тезиса до того, как он доказан, не видна, не усматривается нашей мыслью, но само соответствие тезиса действительности, пусть ещё не дошедшее до уяснения, непременно должно существовать, для того чтобы тезис вообще мог быть доказан.
Если тезис сам по себе истинен, всегда существует возможность доказать его истинность. Возможно, что на первых порах способ доказательства окажется не достигающим цели, ошибочным. В таком случае задача науки заключается в том, чтобы вместо несостоятельного, ошибочного или неточного доказательства истинного тезиса найти другое — правильное, более точное, ведущее к цели. История наук знает немало случаев, когда положения, впоследствии оказавшиеся истинными, первоначально доказывались неточно или даже прямо ошибочным способом, и лишь с новыми успехами науки ошибки в способе доказательства устранялись, а логически неточные способы доказательства заменялись новыми, логически безупречными.
Например, многие доказательства предложений, разработанные античными геометрами, оказались впоследствии недостаточно строгими. Особенно интересно то, что больше всего неточностей оказалось в доказательствах самых первых, элементарнейших предложений. Факт этот легко объясняется. Дело в том, что при доказательстве первых предложений античные геометры в ряде случаев полагались на наглядное представление (или, как иногда называют наглядное представление, на «интуицию»). Так, уже при доказательстве первого предложения первой книги «Начал» (о построении равностороннего треугольника на данной ограниченной прямой) Евклид прибегает для доказательства к построению двух пересекающихся окружностей. Однако, вместо того чтобы строго доказать возможность этой пересекаемости, он просто предполагает эту возможность, опираясь при этом на наглядное представление и не допуская, что оно может быть ошибочным. Пример этот у Евклида — не исключение. Согласно замечанию советского комментатора «Начал» Евклида профессора Д. Д. Мордухай-Болтовского, античные геометрические доказательства имеют настолько явный «полуинтуитивный характер», что из всех составных частей, на которые расчленяется античное геометрическое доказательство, «только один член относится к логической операции, все другие относятся к словесной форме или к чертежу»[11].
Неудивительно поэтому, что в новое время, когда было выяснено, что не всякое наглядное представление безусловно истинно, для теорем, которые доказывались в античной геометрии ссылками на очевидность или наглядность, пришлось разработать более строгие и точные способы доказательства.
Но какой бы ни была степень точности и строгости доказательства, первым условием возможной его безупречности является истинность доказываемого тезиса, т. е. адекватное отражение в нём действительности.
И точно так же для безупречности опровержения первым необходимым условием является действительная ложность опровергаемого положения, его действительное несоответствие фактам. Если опровергаемое положение ложно, то раньше или позже способ его опровержения может быть найден и будет найден. Но если положение, которое пытаются опровергнуть, само по себе истинно, то никакие попытки и ухищрения, какие делаются для его опровержения, не могут привести к цели, и опровергаемое положение останется неопровергнутым.
Убедительным подтверждением сказанного может быть позорное крушение бесчисленных попыток, которые делались и делаются буржуазными социологами и философами для опровержения марксизма. О тщетности этих попыток превосходно говорит в работе «Аграрный вопрос и «критики Маркса»» В. И. Ленин: «Вот уже много лет ученые и ученейшие люди Европы важно заявляют (а газетчики и журналисты повторяют и пересказывают), что марксизм уже сбит с позиции «критикой»,— и тем не менее каждый новый критик опять сначала начинает трудиться над обстреливанием этой якобы уже разрушенной позиции»[12].
2. Основания доказательства (аргументы)
Доказательство осуществлено всюду там, где показывается, что истинность (или ложность) некоторого тезиса необходимо следует из истинности (или ложности) некоторых положений, уже ранее доказанных или признанных истинными, а также из выясненного содержания основных для данной науки понятий.
Все положения, на которые опирается доказательство и из которых — при условии их принятия или признания истинными — необходимо следует истинность доказываемого тезиса, называются основаниями, или аргументами доказательства. Так, при доказательстве теоремы о сумме внутренних углов плоского треугольника основаниями доказательства будет, во-первых, ранее установленное содержание таких понятий геометрии, как «плоский треугольник», «внутренний угол», «смежные углы», «параллельность линий», «внутренние накрест лежащие углы», «соответственные углы». Во-вторых, основаниями доказательства данной теоремы будут некоторые ранее принятые в качестве истинных или ранее доказанные положения геометрии Евклида. Таково принимаемое в геометрии Евклида без доказательства положение, что через точку вне данной прямой в одной с нею плоскости может быть проведена одна и только одна прямая, не пересекающаяся с данной прямой. Таково доказываемое в геометрии Евклида положение о том, что образованные пересечением прямой двух параллельных линий внутренние накрест лежащие и соответственные углы равны между собою. Таково же доказываемое в геометрии Евклида положение о равенстве суммы двух смежных углов двум прямым.
Основаниями (аргументами) доказательства теоремы о сумме внутренних углов треугольника эти положения являются потому, что принятие и доказательство их в качестве истинных с необходимостью приводит к признанию истинным также и положения о равенстве суммы внутренних углов треугольника двум прямым.
Основания (аргументы) доказательства заключают в своём составе положения различного типа. В число оснований входят: а) положения об удостоверенных единичных фактах; б) определения; в) аксиомы, или постулаты, г) доказанные ранее данной наукой положения, или теоремы.
Положения об удостоверенных единичных фактах — чрезвычайно важный вид оснований. За исключением математических наук, опирающихся на факты не непосредственно, но посредством обобщённых понятий об отношениях между объектами, во всех науках доказательство основывается на положениях об удостоверенных — прямо или косвенно— фактах. В огромном числе случаев доказать истинность положения — значит показать, что истинность эта — прямое следствие из положений об известных, хорошо удостоверенных фактах.
И напротив, доказать ложность положения во множестве случаев — значит удостовериться в фактах, противоречащих этому положению.
О значении фактов для доказательства не раз говорили корифеи мировой науки. «Факты.— писал академик И. П. Павлов,— это воздух учёного. Без них вы никогда не сможете взлететь. Без них ваши «теории» — пустые потуги»[13].
И в этом же смысле В. И. Ленин говорил: «Точные факты, бесспорные факты — ...вот что особенно необходимо, если хотеть серьезно разобраться в сложном и трудном вопросе... Факты, если взять их в их целом, в их связи, не только «упрямая», но и безусловно доказательная вещь»[14].
Поэтому безупречность доказательства определяется— в числе прочих условий — уменьем находить факты, либо обосновывающие доказываемое положение, либо не совместимые с ним и тем самым его опровергающие. Особую доказательную силу имеют факты опровергающие. И это вполне понятно. Указания фактов, подтверждающих доказываемое положение, часто бывает ещё недостаточно для строгого доказательства его истинности. Такое указание часто обосновывает истинность положения только в пределах тех фактов, которые были найдены для его подтверждения. Достаточно обнаружить хотя бы один факт, противоречащий доказываемому положению, чтобы обнаружить тем самым полную или, по крайней мере, частичную ложность этого положения.
Если бы факты, подтверждающие доказываемое положение, были сами по себе вполне достаточны для строгого и полного его доказательства, то в таком случае индукция через простое перечисление была бы самым надёжным способом доказательства во всех науках, опирающихся на факты. Известно, однако, насколько ненадёжно, недостоверно всякое обобщение, основывающееся только на том, что в пределах наблюдения пока не обнаружены факты, ему противоречащие. Любой такой факт, найденный впоследствии, сразу опрокидывает или по меньшей мере ограничивает обобщение.
Окружающая нас действительность (особенно это касается общественной жизни) настолько сложна и многообразна, что в подтверждение любого положения, даже явно вздорного, можно подобрать большее или меньшее число отдельных фактов. Однако то обстоятельство, что существуют одновременно и такие факты, которые это же положение опровергают, говорит о том, что единичные факты, будучи взяты сами по себе, в отрыве друг от друга и от окружающих условий, ничего не доказывают.
Поэтому значение оснований доказательства факты получают только тогда, когда они берутся не изолированно, не поодиночке; такое значение факты могут иметь только при условии, если они рассматриваются в их связи и не сами по себе, а как носители общих законов, в этих фактах проявляющихся и ими управляющих.
В состав оснований доказательства входят, кроме положений об удостоверенных фактах, также и определения основных понятий данной науки. В самом деле: доказательство есть переход от положений, уже ранее принятых, к некоторому новому положению, истинность которого необходимо следует из истинности принятых положений. Однако не все из числа этих ранее принятых положений доказываются: некоторые из них представляют собой просто определения основных понятий науки. Так, доказательство теоремы о сумме внутренних углов плоского треугольника в евклидовой геометрии опирается не только на ранее доказанные теоремы о свойствах внутренних накрест лежащих углов, соответственных углов и смежных углов и не только на принимаемое без доказательства положение о параллельных, но также и на определения понятий «плоский треугольник», «внутренние углы плоского треугольника», «параллельные линии», «внутренние накрест лежащие углы», «соответственные углы», «смежные углы», «прямые углы».
Но из того, что определения — в качестве определений — не доказываются, а просто формулируются, отнюдь не следует, будто определения принимаются произвольно или представляют простые «соглашения» относительно смысла тех или иных терминов. Чтобы определение было пригодным для науки, необходимо, чтобы определяемый предмет существовал в самой действительности. Поэтому и в математических науках, и в естествознании, и в науках общественных принятие определения всегда предполагает, что может быть доказано существование характеризованного посредством определения предмета. Условно лишь словесное обозначение предмета (свойства, явления, отношения), но не сам предмет как существующий в действительности. Существование же определяемого предмета может быть и должно быть доказано. Должно быть доказано также соответствие определения определяемому предмету.
Определение понятий необходимо, так как оно — и только оно — даёт возможность во всех рассуждениях, посредством которых в доказательстве совершается переход от доказанного к доказываемому, мыслить входящие в эти рассуждения основные понятия науки в одном и том же содержании и, таким образом, мыслить посредством этих понятий одни и те же предметы.
Наличие определений в составе оснований не значит, однако, будто все определения, необходимые для данного доказательства, непременно формулируются в самом данном доказательстве. Обычно определения формулируются не в каждом данном доказательстве, а в начале изложения науки или, по крайней мере, того раздела науки, к которому относится данное доказательство. Так, в «Началах» Евклида определениями основных понятий начинается каждая книга этого труда. При этом определения в каждой следующей книге новые и не повторяют определений, данных в предыдущих книгах. Но, не появляясь вновь в каждом данном доказательстве, определения понятий, необходимые для точного проведения данного доказательства, непременно им предполагаются и всегда могут быть найдены в соответствующем месте изложения.
Однако из того, что в число оснований, общих для всех доказательств данной науки, входят определения основных понятий данной науки, ещё не следует, будто определению подлежат все без исключения понятия данной науки. И действительно: определить — значит свести неизвестное к известному, сложное к простому. Но есть предметы настолько простые и настолько всем известные, что определить понятия об этих предметах невозможно. Всякая попытка такого определения приводит или к тому, что в определяющем повторяется определяемое (круг в определении), или к тому, что до определения понятное и ясное после определения становится непонятным и неясным.
Таким образом, задача науки в отношении определения понятий, входящих в основания доказательства, состоит в том, чтобы избежать двух противоположных ошибок: 1) не оставить не определёнными те понятия, которые должны быть определены, и 2) не пытаться понапрасну определять те понятия, которые по своей крайней простоте не могут быть определены.
Это правильное понимание задачи определения оснований доказательства хорошо сформулировал Паскаль. В небольшой работе «О геометрическом уме» (De l’esprit géométrique) Паскаль писал: «... порядок, совершеннейший у людей, состоит не в том, чтобы всё определять и всё доказывать, и не в том также, чтобы ничего не определять и ничего не доказывать; но в том, чтобы, держась среднего пути, не определять вещей, ясных и понятных всем людям, но определять все остальные, и не доказывать всех вещей, известных людям, но доказывать все остальные»[15].
Поэтому число определений, входящих в основания доказательств данной науки и формулируемых в начале её изложения, обычно бывает невелико и без нужды не должно быть увеличиваемо.
Положения об удостоверенных фактах и определения входят в число оснований самых различных наук: естественных и общественных.
В математике, механике и теоретической физике кроме определений и удостоверенных фактов в число оснований доказательства входят ещё аксиомы, или постулаты. Так называются положения, которые предполагаются истинными, но в пределах каждой науки в качестве истинных не доказываются.
Так, доказательство теоремы евклидовой геометрии о равенстве суммы внутренних углов плоского треугольника двум прямым опирается не только на ранее доказанную теорему о равенстве суммы двух смежных углов двум прямым, но, кроме того, на теоремы о свойствах внутренних накрест лежащих и соответственных углов, которые в свою очередь опираются на положение, согласно которому через данную точку вне данной прямой в одной с ней плоскости можно провести одну — и притом только одну — прямую, которая ни при каком продолжении её в обе стороны от данной точки не пересечётся с данной прямой. Положение это уже не теорема, а аксиома (постулат). В «Началах» Евклида оно дано (в редакции, отличающейся от приведённой в тексте) в качестве 11-й аксиомы первой книги[16].
Аксиомой (постулатом) это положение является потому, что в «Началах» Евклида оно принимается без доказательства. И действительно: положение это утверждает, что возможно неограниченно продолжить прямую так, чтобы последняя нигде не пересекалась с данной прямой. Но совершенно очевидно, что утверждение это не может быть проверено или доказано: как бы далеко мы ни продолжали прямую, продолжение её будет для нашего наглядного представления ограниченным. В лучшем случае можно сказать, что в тех пределах, в каких прямая продолжена нами, она сохраняет параллельность данной прямой. Но сохранит ли она параллельность и при дальнейшем, ещё нами не воспринятом неограниченном её продолжении,— это остаётся недоказанным.
Аристотель, создавший не только науку логики в целом, но и разработавший, в частности, логическое учение о доказательстве, отличал аксиомы от другого вида недоказываемых наукой положений — от постулатов. Под аксиомами (αρώματα) он разумел такие недоказываемые в данной науке положения, которые в сравнении с другими недоказываемыми положениями являются, во-первых, наиболее общими и, во-вторых, представляют необходимое условие доказательства. Так, в «Метафизике» (кн. III, гл. 2, 997а 5—13) Аристотель говорит, что «не может существовать доказательства для всего», что «все доказывающие науки применяют аксиомы» и что «аксиомы обладают наивысшей степенью общности и представляют начала всего» (Κάρολου γαρ μάλιστα αι πάντων άρΧαι τα αξιώματα έστιν).
Под постулатами (τα αιτήματα, буквально — «требования») Аристотель понимал такие положения, которые, безотносительно к их доказуемости, вводятся в начала науки без доказательства, хотя бы они представлялись учащемуся противными его мнению[17]. Именно потому, что постулат может быть противным мнению учащегося, он вводится в качестве требования: это — положение, которое должно быть принято для того, чтобы были приняты все вытекающие из него выводы.
Постулаты Аристотель отличал от аксиом, но не противопоставлял их аксиомам.
В развитии античной математики после Аристотеля были выработаны три точки зрения по вопросу о различии между аксиомами и постулатами. Эти три точки зрения рассматривает математик и философ Прокл (V век н. э.) в своих «Комментариях» к «Началам» Евклида.
Согласно первой из этих точек зрения, аксиомы — недоказываемые положения, на которые опираются доказательства теорем, а постулаты — недоказываемые положения, на которые опираются построения в геометрии.
Согласно второй точке зрения, аксиомы — допущения, общие для всех наук, а постулаты — специальные допущения, принятые в геометрии. Так, у Евклида в качестве аксиом рассматривались, например, такие положения: «равные одному и тому же равны и между собой», «если к равным прибавляются равные, то и целые будут равные» и т. д. В качестве постулатов у Евклида рассматриваются, например, такие положения: «от всякой точки до всякой точки <можно> провести прямую линию», «из всякого центра и всяким раствором <циркуля> <может быть> описан круг» и т. д.
Зачатки этого понимания различия между аксиомами и постулатами имелись уже у Аристотеля: «Из тех <начал>,— читаем у Аристотеля,— которые применяются в доказывающих науках, одни свойственны каждой науке в отдельности, другие — общи всем...»[18].
Согласно третьей точке зрения, постулаты — в отличие от аксиом — суть «требования», выдвигаемые преподающим науку или руководителем диспута. Постулаты должны быть приняты учащимися или участниками диспута, несмотря на то, что для них требования эти могут представляться не безусловно бесспорными[19].
Впоследствии возобладал взгляд, согласно которому аксиомами должны называться недоказываемые положения не специальные, имеющие силу для всех наук, постулатами же — недоказываемые положения более частные, относящиеся к области какой-нибудь особой специальной науки. Согласно этому взгляду, положение о том, что две величины, равные порознь третьей, равны между собой, рассматривалось в силу его всеобщности как типичная аксиома. Напротив, положение о параллельных вследствие его специально геометрического характера толковалось как типичный постулат.
Распределение аксиом и постулатов в «Началах» Евклида не вполне соответствует этому различению. Хотя ряд постулатов Евклида принадлежит к области геометрия, а ряд его аксиом — к области более общего учения о величинах, последовательное разграничение аксиом и постулатов по степени их специального характера оказывается невозможным. Так, 7-я аксиома первой книги «Начал», утверждающая, что «совмещающиеся друг с другом равны между собой», есть, конечно, аксиома геометрии. Положение о параллельных, принадлежащее к области геометрии, помещалось Евклидом в числе аксиом (11-я аксиома первой книги«Начал») и только позднейшими комментаторами и издателями стало рассматриваться как постулат (5-й постулат той же книги).
В философии и математике XVII века понимание логической природы аксиом и постулатов изменилось. Ряд математиков и логиков этого века сущность аксиом стал видеть в их будто бы безусловной очевидности или самоочевидности. Согласно этому новому взгляду, аксиомы — такие основания доказательства, которые не доказываются в науке не в силу своей общепринятости, а в силу своей полной и безусловной очевидности. Существуют будто бы такие положения, которые, как только на них направляется наш ум, представляются ему с ясностью и очевидностью, исключающими возможность какого бы то ни было сомнения. Будучи совершенно очевидными, положения эти будто не требуют доказательства, ниоткуда не выводятся, представляют истины, непосредственно постигаемые умом, или, другими словами, являются «интуициями», притом интуициями не чувств, а ума. Аксиомы — не просто недоказываемые истины, какими их считали древние математики. Это — истины будто бы недоказуемые. Не нуждаясь ни в каком доказательстве, они составляют последнюю основу всех доказываемых в науке истин. Доказать — значит вывести доказываемое положение или прямо из таких самоочевидных аксиом, или вывести его из положений, которые если не прямо, то в последней инстанции сами опираются на самоочевидные аксиомы и доказываются с их помощью.
В этом учении существенным признаком аксиом провозглашается их непосредственно постигаемая самоочевидность (интуитивность) и их недоказуемость. Напротив, их общепризнанность и более или менее общий для всех наук или специальный характер получает значение свойства, производного от указанных основных свойств.
В связи с этим характерное для античных логиков и математиков понимание различия между постулатами и аксиомами у логиков и математиков XVII века в значительной мере утрачивает прежнее значение. Возникает тенденция к сближению постулатов с аксиомами. Поскольку некоторые постулаты представляются не менее очевидными, чем аксиомы, и поскольку непосредственная очевидность аксиом рассматривается как основание их недоказуемости, такие постулаты по сути уже не отличаются от аксиом и вместе с аксиомами образуют совокупность последних оснований всякого доказательства.
В то же время, однако, некоторые постулаты не поддавались этому сближению с аксиомами по признаку безусловной очевидности. Таков был прежде всего постулат Евклида о параллельных. Уже в самой своей формулировке он содержал понятие о неограниченном продолжении прямой — понятие, которое никак не могло быть признано ни самоочевидным, ни непосредственно постигаемым.
К этому присоединилось ещё и то, что целый ряд начальных положений (теорем и задач на построение) геометрии Евклида доказывался и решался вовсе без участия постулата о параллельных. Только в двадцать девятом предложении первой книги «Начал» постулат Евклида впервые использовался в качестве одного из оснований доказательства этого предложения.
Эта далеко не безусловная «очевидность» постулата о параллельных, а также «позднее» появление его в числе оснований, на которые опираются доказательства теорем геометрии Евклида, в сопоставлении со взглядом на аксиомы, как на истины самоочевидные, уже давно внушали математикам мысль — не является ли этот постулат теоремой, которая может быть доказана.
Попытки доказать 5-й постулат Евклида предпринимались ещё античными математиками и продолжались до Лобачевского. Великий русский математик во второй половине 20-х годов прошлого века пришёл к гениальному открытию, которое повлекло за собой коренную переработку взгляда логики на природу аксиом и на их значение для доказательства.
В начале своих исследований, посвящённых теории параллельных, Лобачевский пытался доказать постулат Евклида способом от противного. Предполагая, в противоречии с постулатом Евклида, что через точку вне данной прямой в одной с ней плоскости можно провести не одну единственную прямую, не пересекающуюся с данной, Лобачевский надеялся, что, развивая следствия из этого предположения, он придёт в конце концов к следствию, опровергающему это предположение и тем самым доказывающему истинность самого постулата Евклида.
Но никакие следствия, развиваемые из предположения, противоречащего постулату Евклида, не могли доказать абсурдность этого предположения. Никаких противоречий между теоремами, доказанными на основе предположения, противоречащего постулату Евклида, не получалось.
В конце концов Лобачевский убедился, что все старания ряда математиков доказать постулат Евклида, т. е. вывести его как следствие из других аксиом и постулатов Евклида, были ошибочны не только по выполнению, но и по замыслу. Постулат о параллельных оказался независимым от остальных аксиом и постулатов Евклида. С другой стороны, как уже говорилось выше, постулат этот не обладает и безусловной очевидностью. Тем не менее постулат Евклида является одним из оснований классической системы геометрии, не заключающей нигде в своих доказываемых с помощью этого постулата положениях никаких противоречий.
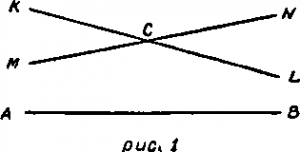
Небезусловная очевидность постулата Евклида и отсутствие противоречий в системе теорем, доказываемых на основе постулата, противоречащего постулату о параллельных, даёт возможность поставить вопрос, каков будет результат, если вместо постулата Евклида в число оснований геометрии будет принят другой — тоже не безусловно очевидный — постулат. Согласно последнему, получившему название постулата Лобачевского, через данную точку С, лежащую вне данной прямой АВ, можно провести в одной с ней плоскости не одну единственную не пересекающуюся с прямой АВ прямую, как это утверждает постулат Евклида, а целый пучок прямых, заключающийся между двумя прямыми KL и MN, проходящими через данную точку (см. рис.1) и называемыми параллельными относительно АВ[20].
Исследования Лобачевского показали, что замена постулата Евклида постулатом Лобачевского приводит к выявлению новой системы геометрии, получившей название геометрии Лобачевского и оказавшейся одним из видов так называемой неевклидовой геометрии. В геометрии Лобачевского сохраняются все определения, аксиомы и постулаты геометрии Евклида, кроме 5-го постулата, или 11-й аксиомы. Последний заменяется постулатом Лобачевского. Доказательства теорем развиваются безупречно строго в полную систему геометрии, которая нигде не приводит ни к каким противоречиям. По содержанию теоремы геометрии Лобачевского делятся на два класса: во-первых, теоремы, доказываемые без помощи постулата Лобачевского (так называемая абсолютная геометрия), и, во-вторых, теоремы, доказываемые с помощью этого постулата. Первые ничем не отличаются от соответствующих теорем Евклида. Вторые отличаются, а именно: разность в численных результатах этих теорем сравнительно с результатами теорем Евклида тем больше, чем больше масштаб соответствующего геометрического объекта. Например, по Евклиду, сумма внутренних углов плоского треугольника равна двум прямым. По Лобачевскому, эта сумма меньше двух прямых. При этом разность эта тем больше, чем больше данный треугольник.
Открытие Лобачевским неевклидовой геометрии означало эпоху не только в развитии математики, но также и в развитии логического учения об аксиомах как об основаниях доказательства. Это открытие Лобачевского нанесло смертельный удар идеалистическим теориям рационалистов и кантианцев. Логики этого направления сущность аксиом полагали в их интуитивной, т. е. непосредственной очевидности, в их априорной, т. е. будто бы предшествующей всякому опыту, безусловной и необходимой наглядности. Так как, по Канту, истины математики имеют, во-первых, всеобщий и необходимый характер, во-вторых, основываются на априорных формах чувственной интуиции, то ни о какой неевклидовой геометрии, разумеется, не может быть и речи.
Напротив, по Лобачевскому, вопрос о том, какие аксиомы или постулаты должны быть приняты в число оснований всей системы доказательств данной науки, определяется отнюдь не априорными формами интуиции. Такие положения геометрии, как постулат Евклида или постулат Лобачевского, отнюдь не безусловно самоочевидны.
Так как аксиомы не обладают безусловной очевидностью, то для решения вопроса о том, какие из небезусловно очевидных положений будут в данной науке доказываться, а какие будут приняты в ней без доказательства, т. е. в качестве аксиом,— необходимо некоторое основание.
Таким основанием не может быть произвол, условное соглашение, субъективная точка зрения. Если в числе оснований данной науки имеются аксиомы, то в такой науке основанием для выбора системы или группы аксиом, входящих в начальные основания науки, являются следующие требования:
1. Выбранная группа аксиом должна представлять группу допущений, между которыми нет противоречий. Другими словами, группа аксиом должна быть такова, чтобы, опираясь на неё, нельзя было доказать суждение и отрицание этого суждения.
2. Выбранная группа аксиом должна быть такова, чтобы из неё (а также из принятых наукой определений) могла быть последовательно выведена вся совокупность теорем данной науки. При этом число аксиом не должно превышать того, какое необходимо и достаточно, чтобы с помощью данной группы аксиом могли быть доказаны все теоремы данной науки.
3. Ни одна из принятых в данной науке аксиом не может быть получена как вывод ни из какой другой аксиомы или других аксиом той же науки, т. е. каждая аксиома должна быть предположением вполне независимым от предположений, выражаемых всеми другими аксиомами данной науки.
Последнее свойство аксиом нуждается в объяснении. Свойство это нельзя понимать так, будто аксиома вообще не может быть выводима ни из каких других положений. Аксиома не может быть выводима из других аксиом только в рамках данной системы науки. Так, 11-я аксиома Евклида (постулат о параллельных) не может быть выведена из других аксиом геометрии Евклида. Именно поэтому все попытки доказать эту аксиому в рамках геометрии Евклида с её аксиомами и постулатами потерпели неудачу.
Но можно взять другую систему или группу аксиом геометрии. Можно выбрать такую группу аксиом, что постулат о параллельных, который в системе геометрии Евклида является независимой аксиомой, будет в этой другой системе теоремой, выводимой из принятых в этой системе аксиом.
Таким образом, аксиоматическое значение некоторых положений науки не есть безусловное свойство этих положений. Разница между аксиомой и теоремой — не безусловная. Положение, которое в одной системе науки будет аксиомой, оказывается теоремой в системе науки с другой совокупностью аксиом. И наоборот: положение, доказываемое в данной системе науки как её теорема, не доказывается, а принимается в качестве аксиомы в системе науки с другой совокупностью аксиом.
В конечном счёте выбор той или другой группы аксиом (или постулатов) в качестве принятой в науке системы оснований её доказательств обусловливается и оправдывается не самоочевидностью этих оснований, а всей суммой результатов, к которым приводят доказательства науки, опирающиеся на принятые аксиомы и постулаты. Только содержательная плодотворность результатов, полученных с помощью принятой в данной системе науки группы аксиом, составляет основание для их выбора. Тем самым выбор оснований для всей системы доказательств науки — выбор аксиом или постулатов — связывается с проверкой этих оснований по их результатам, связывается с материальной практикой, с опытом.
Таким образом, с точки зрения современной логики, опирающейся на данные новейшей науки, аксиомами называются положения, не доказываемые в данной науке и играющие в ней — наряду с определениями основных понятий — роль допускаемых оснований всех доказываемых в науке истин. Роль эту аксиомы играют не в силу своей безусловной очевидности, хотя некоторые аксиомы представляются очевидными, и тем более не в силу своей априорности, так как никаких априорных положений нет ни в какой науке. Аксиомы данной науки выбираются в качестве аксиом. Однако основанием для выбора является не субъективный произвол, не «удобство», не «соглашение», а способность выбранной группы аксиом доказать всю совокупность известных истин науки, оправданных в своих результатах, т. е. в конечном счёте удостоверенных в своей истинности материальной практикой.
То, что в аксиомах не следует видеть истины безусловно недоказуемые, было не раз показано классиками марксизма-ленинизма. Энгельс говорит, что, например, аксиомы математики «доказуемы диалектически, поскольку они не чистые тавтологии»[21]. И точно также Ленин поясняет в конспекте «Науки логики» Гегеля, что фигуры силлогизма могли получить значение аксиом только после того, как значение это было доказано в миллиардах случаев опытом: «практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом»[22].
Таким образом, и аксиомы как части оснований доказательства отнюдь не «возвышаются» над опытом, отнюдь не «предшествуют» опыту, а составляют результат материальной практики и опыта, лежащего в основе доказательства.
Все указанные выше требования, предъявляемые при выборе аксиом, имеют силу, разумеется, только в отношении тех наук, которые имеют в числе своих оснований аксиомы (постулаты) или, как говорят, допускают аксиоматическое построение. Таковы математика, теоретическая физика. Но существует обширный класс наук, в которых аксиоматическое построение неприменимо. В этих науках аксиомы (постулаты) не входят в число оснований науки» Такова, например, история.
В число оснований доказательств, кроме положений об удостоверенных фактах, на которые опирается доказываемый тезис, кроме определений основных понятий науки и аксиом, входят ещё доказанные ранее положения науки, необходимые для обоснования тезиса.
Так, при доказательстве теоремы евклидовой геометрии о сумме внутренних углов плоского треугольника в качестве оснований доказательства используют не только определения понятий, например понятий о параллельных, о смежных углах о внутренних накрест лежащих углах, о соответственных углах, и не только аксиомы, например аксиому (постулат) Евклида о параллельных. В качестве оснований доказательства этой теоремы используют также доказанную до неё теорему о равенстве суммы смежных углов двум прямым.
Рассматривая доказательство, нетрудно убедиться, что ранее доказанные положения, на которые опирается доказываемый тезис, используются в ходе доказательства либо непосредственным, либо опосредствованным образом.
Непосредственно используются те положения, на которые прямо ссылаются в ходе доказательства, как на положения, из истинности которых следует истинность доказываемого тезиса. Так, одним из положений, непосредственно используемых для доказательства теоремы Пифагора, будет 41-я теорема первой книги Евклида. Теорема эта утверждает, что если параллелограмм имеет с треугольником одно и то же основание и находится между теми же параллельными, то параллелограмм будет вдвое больше треугольника. Теорема эта принадлежит к непосредственным основаниям теоремы Пифагора, так как при доказательстве последней Евклид дважды ссылается в самом ходе доказательства на 41-ю теорему. Иными словами, 41-я теорема прямо входит в число оснований, истинность которых приводит к признанию истинности теоремы Пифагора.
Опосредствованным образом используются для доказательства те положения, на которые в самом ходе данного доказательства прямо не ссылаются, но при помощи которых были ранее доказаны непосредственные основания данного доказательства. Положения эти могут быть названы предшествующими основаниями доказательства. Так, для той же теоремы Пифагора одним из таких ранее доказанных, или предшествующих, оснований её доказательства будет 38-я теорема первой книги Евклида. Теорема эта утверждает, что треугольники, находящиеся на равных основаниях и между теми же параллельными, равны между собой. Эта теорема не входит в число непосредственных оснований доказательства теоремы Пифагора, так как в ходе этого доказательства Евклид на 38-ю теорему не ссылается. Но она входит в число оснований доказательства опосредствованным образом, будучи одним из оснований, при помощи которых была доказана 41-я теорема. А эта последняя есть, как мы уже знаем, одно из непосредственных оснований доказательства теоремы Пифагора.
Чем дальше развивает наука доказательства своих положений, тем большим становится число предшествующих оснований доказательства каждого нового положения. Если, рассматривая данный тезис науки, мы задались бы целью выяснить все основания, на которые опирается его доказательство, то оказалось бы, что непосредственные основания его доказательства опираются на некоторые предшествующие им основания, эти последние — в свою очередь на другие предшествующие основания и т. д. Однако, каким бы большим ни было число предшествующих оснований данного доказательства, оно не может быть бесконечным. Рано или поздно мы дойдём до таких предшествующих оснований, которые ни из каких предшествующих им оснований уже не могут быть выведены.
Основания доказательства, которые не могут быть выведены ни из каких предшествующих им оснований, называются начальными основаниями данной науки.
Начальными основаниями для данной науки являются: положения об удостоверенных единичных фактах, определения и аксиомы (постулаты). Теоремы не могут быть начальными основаниями, так как начальные основания ниоткуда не выводятся; напротив, всякая теорема — доказываемое положение, а все доказываемые положения выводятся из оснований непосредственных или предшествующих.
Все определения и аксиомы, которые могут встретиться в отдельных доказательствах в качестве непосредственных оснований или к которым доказательство может быть возведено как к своим предшествующим основаниям, входят в число начальных оснований науки. При этом, однако, в доказательства эти основания входят в каждом отдельном случае лишь частично. Так, доказательство, например, теоремы Пифагора опирается непосредственно не на все, а лишь на некоторые аксиомы, не на все, а лишь на некоторые определения, входящие в круг начальных аксиом и определений.
Напротив, в числе начальных оснований науки находится не часть аксиом, а все аксиомы данной науки, не часть определений, а все её определения.
Чем дальше отстоит доказываемое положение от начальных оснований данной науки, тем большим становится число предшествующих оснований доказательства. И действительно: каждое доказанное ранее положение, на которое в данном доказательстве наука ссылается, как на одно из непосредственных оснований доказываемого тезиса, обусловлено, в свою очередь, длинным рядом предшествующих ему положений. Ни на одно из них в пределах данного доказательства не ссылаются — иначе доказательство каждой теоремы было бы повторением всего предшествующего этой теореме содержания науки со всеми её доказательствами. В то же время все они могут быть найдены в соответствующем месте системы науки, где они полностью излагаются, иначе основание, на которое опирается доказываемое положение, само было бы -недоказанным.
Наличие в далеко продвинувшейся науке длинной цепи не непосредственных оснований, предполагаемых каждым непосредственным основанием любого доказательства, делает особенно важным условием состоятельности доказательства истинность всех оснований доказываемого тезиса.
В самом деле, непосредственное для данного доказательства основание есть только звено предшествующей ему цепи обусловливающих его оснований. Если эта цепь длинна и если какое-нибудь из её звеньев окажется ложным, то и заключительное звено — данное непосредственное основание доказательства — тоже может оказаться ложным. А в таком случае и доказываемый тезис, как опирающийся на ложное основание, может оказаться ложным.
Поэтому в качестве оснований доказательства должны быть принимаемы только истинные, строго доказанные, проверенные и удостоверенные в своей истинности положения. Любой вид оснований, вообще говоря, сказывается на истинности результата. Поэтому ни входящие в число оснований доказательства положения об удостоверенных фактах, ни определения основных понятий науки, ни аксиомы, ни уже ранее доказанные положения науки не должны быть ложными. Основания доказательства не должны быть даже сомнительными. Сомнительность основания есть по крайней мере возможность его ложности, а возможность ложности в основаниях доказательства делает возможным ложность самого доказываемого тезиса. Поэтому доказательство, опирающееся на сомнительные основания, не есть, строго говоря, подлинное доказательство. Только вполне удостоверенная истинность всех оснований, на которые опирается доказательство, делает доказательство (при соблюдении всех прочих условий и правил, о которых речь впереди) путём и средством к отысканию новой истины.
3. Способ доказательства (демонстрация)
Мы рассмотрели две составные части доказательства: доказываемый тезис и основания доказательства. Мы видели, что главная задача доказательства — сделать непреложной либо истинность доказываемого, либо ложность опровергаемого. Мы видели также, что истинность доказываемого или ложность опровергаемого тезиса не могут быть обнаружены непосредственно. Чтобы убедиться в истинности доказываемого тезиса, следует указать истинное основание, признав которое истинным, мы с необходимостью должны признать истинным также и доказываемый тезис.
Однако, хотя указание истинных оснований для выяснения истинности доказываемого тезиса необходимо, но одним лишь этим мы ещё не достигаем цели доказательства. Только в немногих случаях указание истинных оснований даёт истинность доказываемого тезиса сразу, в виде непосредственного вывода. Так, если требуется доказать, что некоторые из равных между собой углов — прямые углы, то для доказательства истинности этого утверждения достаточно сослаться, как на основание, на истину о том, что все прямые углы равны между собою. Из этого основания сразу, непосредственно, по законам одной лишь логики (а именно — согласно правилам обращения) получается истинный вывод, что некоторые из равных между собой углов — прямые.
Но в огромном большинстве случаев знания истинных оснований, ведущих к признанию истинности тезиса, недостаточно. Необходимо кроме того показать, какова связь, необходимо ведущая от истинности данных оснований к истинности обусловленного ими тезиса. Связь эта во многих случаях непосредственно не видна и требует выяснения. Так, если ученик знает все определения, все аксиомы и все теоремы, из истинности которых, как из оснований, выводится истинность теоремы Пифагора, это ещё не значит, что ученик знает доказательство теоремы Пифагора. Для знания доказательства требуется, чтобы ученик знал, какова связь между всеми известными ему порознь основаниями теоремы Пифагора,— другими словами, какова последовательность оснований и выводов из оснований, необходимо ведущая к признанию истинности доказываемого в этой теореме положения.
Последовательность, или связь оснований и выводов из оснований, имеющая результатом необходимое признание истинности доказываемого тезиса, называется способом доказательства у или демонстрацией. Демонстрация есть не составная часть доказательства, но третья, наряду с доказываемым тезисом и основаниями, логическая характеристика доказательства.
Из этого определения демонстрации видно её отличие от составных частей доказательства— тезиса и основания. И тезис и каждое из оснований — положение об удостоверенном факте, определение, аксиома, ранее доказанное положение науки — представляют собой отдельное суждение. Напротив, демонстрация никогда не есть ни отдельное суждение, ни простая сумма отдельных суждений. Демонстрация всегда есть логическая связь суждений, приводящая к определённому логическому результату. Демонстрация это более или менее длинная цепь умозаключений у посылками которых являются основания данного доказательства, а последним заключением — доказываемый тезис у который, таким образом, удостоверяется в качестве истинного.
Так, при доказательстве теоремы евклидовой геометрии о сумме внутренних углов треугольника (см. рис. 2) мы сначала продолжаем сторону треугольника АВС, например сторону АС до точки Е. Затем проводим из точки С прямую CD, параллельную АВ и по одну с ней сторону от прямой АС. Затем мы рассуждаем следующим образом. Прямая ВС пересекает параллельные (по построению) прямые АВ и CD. Следовательно, углы АВС и BCD будут равны как внутренние накрест лежащие. Прямая АС пересекает те же—параллельные по построению — прямые АВ и CD. Следовательно, углы ВАС и DCE равны как соответственные. Угол ВСЕ, представляющий сумму углов BCD и DCE, равен сумме двух внутренних углов треугольника (АВС и ВАС), так как угол BCD равен углу АВС, а угол DCE равен углу ВАС. Прибавим к углу ВСЕ угол ВСА — третий внутренний угол треугольника АВС. Тогда сумма углов DCE, BCD и ВСА будет равна сумме внутренних углов данного треугольника: углов ВАС, АВС и ВСА. Но так как сумма углов ВСЕ (равного сумме углов ВАС и АВС) и ВСА равна сумме двух смежных углов, а эта сумма равна двум прямым углам, то сумма внутренних углов ВАС, АВС и ВСА в треугольнике АВС также равна двум прямым.
Всё в целом это рассуждение — демонстрация. Основания доказательства не выделяются в группу положений, отдельных от демонстрации, но появляются каждое на том месте, какое определяется для него логической связью всех звеньев демонстрации.
Так как демонстрация — порядок связи между основаниями и тезисом— порядок, непросто усматриваемый из оснований, но такой, который ещё должен быть найден, то доказательство одного и того же положения науки может быть более или менее сложным или простым, громоздким или кратким и т. д. Самый порядок, план доказательства может варьироваться.
Связь оснований, ведущая к усмотрению истинности доказываемого тезиса,— не единственная. А так как связь эта не дана вместе с самими основаниями, но ещё должна быть открыта, выяснена, найдена, то доказательство есть творческая задача науки, которая творческими же средствами и решается.
В ряде частных случаев задача доказательства оказывается настолько сложной, что разрешение её требует от учёных огромных усилий на протяжении целых десятилетий или даже столетий. До сих пор не найдено доказательство теоремы Ферма о том, что уравнение xn = yn+zn не может иметь решений для всех целых значений n больших дЕух. В течение почти двух с половиной тысячелетий оставалось недоказанным существование атома, пока успехи новейшей экспериментальной и теоретической физики не принесли, наконец, это доказательство. Гениальная догадка Джордано Бруно о существовании планет, обращающихся вокруг других звёзд, получила доказательное подтверждение только в последние десятилетия. Во всех этих случаях учёным пришлось приложить немало усилий для доказательства того, что могло быть доказано лишь при определённых условиях развития наблюдения, эксперимента и теоретического анализа.
С другой стороны, там, где задача доказательства успешно разрешалась, пути и средства её разрешения у разных учёных были неодинаковы. Уже античная математика знала не одно единственное доказательство теоремы Пифагора, а целый ряд таких доказательств. И это типично для доказательства. Доказываемый тезис — один, логические законы мышления — одни, но способы, ведущие к признанию истинности тезиса, могут быть разные. Способы эти определяются: 1) основаниями, из которых выводится тезис, 2) связью между основаниями и тезисом. Связь эта не видна из оснований, отдельно взятых. Она находится посредством рассмотрения отношений между доказываемым тезисом и тем, что уже ранее было доказано.
Но так как от доказываемого тезиса к уже доказанным положениям можно перейти не одним единственным способом, доказательство способно к развитию и совершенствованию. От примитивных способов доказательства, опиравшихся на неточные, приблизительные и потому часто ошибочные наглядные представления, до современных доказательств, опирающихся на точно определённые понятия, на не зависящие одна от другой, свободные от противоречий, достаточные в своём числе аксиомы, а также на чрезвычайно строго доказанные теоремы, практика доказательства прошла большой путь уточнения и совершенствования. Соответственным образом изменилась, уточнилась и логическая теория доказательства.
V. Виды доказательства
Доказательства делятся на виды в зависимости от: 1) цели доказательства, 2) способа доказательства и 3) роли опытных данных как оснований доказательства.
1. Различие доказательств по цели доказательства
В отношении цели доказательство может быть или доказательством истинности, или доказательством ложности некоторого положения. Доказательство, имеющее целью установление истинности тезиса, называется просто доказательством. Доказательство, имеющее целью установление ложности тезиса, называется опровержением.
С логической точки зрения опровержение есть доказательство того, что между опровергаемым положением и другими положениями, о которых известно, что они истинны, существует отношение противоположности. Так как два противоположных суждения не могут быть — согласно закону противоречия — оба сразу истинными, то из истинности суждений, противоположных опровергаемому, необходимо следует ложность опровергаемого положения. С этой точки зрения опровергнуть данное положение — значит найти такие положения, которые были бы противоположны данному и о которых было бы известно, что они истинны.
Такие противоположные опровергаемому и вместе с тем истинные положения могут быть либо суждениями о воспринимаемых или удостоверенных фактах, либо суждениями, доказанными на основании других истинных суждений.
Так, если американская пропаганда силится доказать, будто США стоят за мир, то это лживое утверждение опровергается указанием на факты, противоречащие ему. Такими известными всему миру фактами являются: создаваемые американцами во всех частях света военные базы; отказ правительства США от встречи глав великих держав с целью обсуждения всех спорных вопросов, имеющих значение для ослабления международного напряжения; поддержка правящими кругами США реакционных сил во всех странах; засылка шпионов и диверсантов в страны демократического лагеря и т. д. и т. п. Здесь опровержение достигается путём сопоставления опровергаемого положения с положением об удостоверенных фактах.
Но противоположные опровергаемому истинные положения могут быть не только суждениями, полученными из восприятия или удостоверения фактов. Они могут быть также суждениями, доказанными в качестве истинных на основании других истинных суждений. Так, положение о том, что ко всякой кривой можно провести касательную, опровергается путём сопоставления этого положения с противоречащим ему положением о существовании непрерывных функций, не имеющих производной. Но последнее положение доказывается на основании ряда других истинных положений.
Следует заметить, что опровержение того или иного суждения не зависит от того, будет ли противопоставляемое ему противоположное истинное суждение противоречащим или противным (контрарным)[23]. Так, положение о том, что «ни одно растение не питается животными», опровергается противопоставлением ему истинного положения о существовании растений, которые питаются или насекомыми, или рачками, личинками комаров, инфузориями и т. д. Здесь ложность опровергаемого общего суждения выводится из истинности противоречащего ему частного суждения.
Напротив, положение естествоиспытателей-метафизиков, что «ни один вид не изменяется и не переходит в другой», оказалось опровергнутым, когда было доказано, что «все виды изменяются и способны переходить в другие виды». Здесь ложность опровергаемого общего суждения выводится из доказанной истинности противного общего суждения.
Возможность опровержения ложного суждения путём противопоставления ему не только истинного противоречащего, но также и истинного противного (контрарного) суждения — вполне понятна. Опровержение, как мы уже знаем, состоит в выводе о ложности опровергаемого суждения из истинности некоторого другого суждения. Но возможность заключения от истинности данного суждения к ложности противоположного ему суждения не зависит от вида противоположности. Заключение это основывается на законе противоречия, а этот закон распространяется и на противоречащую и на противную противоположности.
Опровержение — часто применяемый вид доказательства. И в практической жизни и в науке, поставленной на службу жизни, поиски истины неотделимы от опровержения заблуждения. Истина пускает корни только в почву, очищенную от лжи и заблуждения. История науки в бесчисленных случаях доказывает, что условием движения науки вперёд является непримиримая борьба с тем, что противоположно истине, т. е. устранение заблуждения. Наука, подлинная, передовая наука, не отделяющая себя от народа, работающая на благо народа, несовместима ни с каким заблуждением ни в какой области знания. Разумеется, для полного искоренения заблуждения одного лишь противопоставления истины заблуждению недостаточно. Жизненным основанием и корнем заблуждения в классовом обществе часто оказывается практический интерес реакционных классов. Именно реакционный классовый интерес побуждает ныне буржуазных деятелей науки извращать истину и насаждать заблуждение. В противоположность этому рабочий класс всегда заинтересован в установлении истины и искоренении заблуждения.
Но как бы ни была велика роль практического интереса в деле устранения заблуждения, без теоретического разоблачения лжи борьба истины против заблуждения не только не может быть завершена, но даже не может быть и начата. Необходимым логическим средством и условием этой борьбы является опровержение.
2. Различие доказательств по способу доказательства
По способу доказательства каждое доказательство бывает или прямое, или косвенное.
Прямое доказательство ведёт через рассмотрение оснований и через рассмотрение выводов, опирающихся на основания, к усмотрению истинности доказываемого тезиса. Схема этого вида доказательства: из данных оснований (а, b...) необходимо следуют положения (k, l...); из этих последних необходимо следует доказываемый тезис p. Так как все основания доказательства (а, b...) — истинны и так как логическая связь, ведущая от (а, b...) через (k, l...) к положению p, — правильная, то доказываемый тезис p — истинен.
Прямое доказательство устанавливает истинность доказываемого тезиса посредством исследования самого доказываемого тезиса. Исследование это выясняет, что так как доказываемый тезис необходимо следует из некоторых положений и так как положения эти истинны, то доказываемый тезис также будет истинным.
Косвенное доказательство устанавливает истинность доказываемого тезиса, исследуя не самый доказываемый тезис, а некоторые другие положения. Эти положения так связаны с доказываемым тезисом, что из установления их ложности необходимо вытекает истинность доказываемого тезиса. Поэтому в косвенном доказательстве задача состоит в выяснении ложности положений, обусловливающей истинность доказываемого тезиса.
Косвенное доказательство бывает или разделительным, или апагогическим.
В разделительном косвенном доказательстве доказываемый тезис рассматривается как одно из некоторого числа предположений, в своей сумме исчерпывающих все возможные по данному вопросу предположения. Доказательство состоит в том, что все эти предположения опровергаются, кроме одного, которое и есть доказываемый тезис. Тем самым доказывается, что этот тезис, как единственное из всех возможных предположений, которое осталось неопровергнутым, должен быть истинным.
Если, например, установлено, что имело место преступление, которое непосредственно могли совершить только лица А, В, С и D, и если, кроме того, установлено, что ни В, ни С, ни D непосредственно не совершили его, то тем самым доказано, что преступление непосредственно совершило лицо А.
Условием логической безупречности разделительного доказательства является полнота перечисления и, соответственно, полнота исследования всех возможных по данному вопросу предположений. Только при этом условии опровержение всех рассмотренных предположений, кроме одного, означает необходимую истинность этого последнего оставшегося неопровергнутым предположения. Так, возвращаясь к рассмотренному примеру, необходимо заметить, что виновность А в непосредственном совершении раскрытого преступления необходимо вытекает из опровергнутой виновности В, С и D лишь при условии, если установлено, что только А, В, С и D могли непосредственно совершить данное преступление. Но если бы оказалось, что по обстоятельствам данного случая преступление могло быть непосредственно совершено также и лицом Е, то опровержение виновности В, С и D, разумеется, ещё не доказало бы виновности А, так как виновным может оказаться Е.
В математических науках разделительное доказательство применяется очень часто, так как в этих науках особенно легко достижимо исчерпывающее перечисление всех видов данного рода или всех предположений, возможных в исследуемом случае.
В науках нематематических применение разделительной формы доказательства обусловлено возможностью исчерпывающего перечисления всех возможных положений, одним из которых является доказываемый тезис. В этих науках часто невозможно заранее перечислить и учесть все эти положения. В таких случаях, если пренебречь тем, что не имеется необходимых условий для строгого разделительного доказательства, легко возникает ошибка необоснованного заключения, которое может оказаться ложным. Но даже если бы выведенное заключение случайно оказалось соответствующим действительности, истинность его осталась бы в данном случае недоказанной.
Апагогическое косвенное доказательство устанавливает истинность доказываемого тезиса посредством опровержения противоречащего ему положения. Из ложности последнего следует — на основании закона исключённого третьего — истинность доказываемого тезиса. В математических науках апагогическое доказательство принимает особую форму, называемую обычно «доказательством от противного». Название это, общепринятое в математике. не точно, так как в этих доказательствах истинность доказываемого тезиса выводится из ложности не противного, а противоречащего ему тезиса[24].
Косвенное апагогическое доказательство имеет две части. Сначала при помощи особого приёма доказывается ложность тезиса не-p, противоречащего доказываемому тезису р. А именно: предполагают, что тезис не-р, противоречащий доказываемому, — истинен. Этот противоречащий тезис (не-p) вводится в число оснований доказательства (а, b, с, d), о которых известно, что они истинны. Затем из получившихся таким образом оснований (а, b, с, d..., не-p) развивают ряд необходимо следующих из них выводов. Выводы эти развивают до тех пор, пока не получится какое-нибудь заключение, противоречащее одному из оснований, например основанию а. Так как два противоречащих друг другу положения не могут быть — по закону противоречия — оба сразу истинными, и так как известно, что положение а — истинно, то заключение не-a необходимо должно быть ложно. Итак, развивая выводы из принятых оснований, мы получили ложное заключение не-a. Но заключение не-a может быть ложно или оттого, что ложно какое-нибудь из оснований, на которые опирается не-а, или оттого, что логическая связь между основаниями (а, b, с, d..., не-p) и заключением (не-а) — неправильная. Так как в нашем случае логическая связь (по предположению) — правильная, и так как известно, что все основания, кроме не-р,— истинны, то ложным должно быть положение не-р.
Такова первая часть, или стадия, косвенного апагогического доказательства. Эта первая стадия выявляет ложность сделанного вначале предположения об истинности тезиса, противоречащего доказываемому. Поэтому первая часть косвенного доказательства называется reductio (deductio) ad absurdum, т. e. «приведение к нелепости».
Вторая стадия косвенного апагогического доказательства очень краткая. Предположенный истинным тезис не-p оказался ложным. Но тезис этот— противоречащий по отношению к доказываемому. На основании закона исключённого третьего из ложности суждения необходимо следует истинность противоречащего ему суждения. Поэтому из установленной ложности не-p необходимо следует истинность р, т. е. истинность того самого положения, которое должно было быть доказано.
Такова схема косвенного, апагогического доказательства.
Примером такого доказательства может быть доказательство известного правила первой фигуры простого категорического силлогизма. Согласно этому правилу, меньшая посылка первой фигуры должна быть утвердительной. Доказывается это следующим образом.
Предположим, что меньшая посылка первой фигуры может быть отрицательной, т. е. предположим, что истинен тезис, противоречащий доказываемому. Все остальные условия и правила первой фигуры, доказанные теорией силлогизма в качестве истинных, оставим в силе и, присоединив к ним предположение, будто меньшая посылка может быть отрицательной, посмотрим, какие выводы последуют из всех этих положений.
Если меньшая посылка (S—М) — отрицательная, то, согласно общим правилам силлогизма, заключение (S—Р) также будет отрицательное. Как известно из правил распределённости терминов, в отрицательном суждении предикат всегда распределён. Но предикат заключения является большим термином силлогизма. Согласно общим правилам силлогизма, если больший термин (Р) распределён в заключении, то он должен быть распределённым и в большей посылке. Но в этой посылке больший термин, будучи её предикатом, может быть распределённым только в том случае, если она отрицательна.
Однако (по предположению) меньшая посылка (S—М) тоже отрицательная. Так как, согласно общим правилам силлогизма, отрицательной может быть только одна посылка, то заключение об отрицательности большей посылки — ложно.
Обнаружившаяся ложность заключения может быть обусловлена либо логической ошибкой в выводе, либо ложностью оснований. Однако в данном случае вывод сделан правильно. С другой стороны, все основания, кроме предположения об отрицательности меньшей посылки, представляют собой заведомо истинные и строго доказанные логические правила теории суждения и силлогизма. Отсюда следует, что сделанное вначале предположение об отрицательности меньшей посылки — ложно. А так как ложное предположение об отрицательности меньшей посылки противоречит положению о её положительности, то, согласно закону исключённого третьего, из доказанной ложности предположения об отрицательности меньшей посылки необходимо следует её утвердительность.
Опровержения, так же как и простые доказательства истинности тезиса, могут быть как прямыми, так и косвенными.
Условием прямого опровержения является доказательство истинности положения, противоположного опровергаемому тезису. Из истинности положения, противоположного опровергаемому тезису, на основании закона противоречия следует ложность самого опровергаемого тезиса. При этом истинное положение, противопоставляемое опровергаемому, может быть как противоречащим, так и противным. И действительно: заключение от истинности противопоставляемого положения к ложности опровергаемого делается на основании закона противоречия, который относится не только к противоречащим, но и к противным суждениям.
Если опровергаемое прямым способом положение — общее, то для опровержения его достаточно доказать истинность противоположного ему частного положения. Так, чтобы убедиться в ложности общего суждения о том, что все славянские языки имеют формы склонения имён, достаточно узнать об отсутствии форм склонения, например в именах болгарского языка. Так как противоположность здесь — противоречащая, то из истинности частного будет следовать необходимая ложность общего.
Но если опровергаемое прямым способом положение — частное, то для опровержения его уже недостаточно установить истинность противостоящего ему частного положения. Такая противопоставленность, будучи подпротивной, не допускает применения закона противоречия, а потому, доказав истинность частного положения, противостоящего опровергаемому, мы ещё не получим права заключать о ложности опровергаемого положения — тоже частного. Так, желая доказать ложность частного суждения «некоторые языки являются надстройкой над базисом», мы не можем удовлетвориться доказательством того, что «некоторые языки не являются надстройкой над базисом». Доказательство истинности этого частного положения не позволяет сделать заключение о ложности противостоящего ему частного положения: как подпротивные, оба суждения могут оказаться истинными. В этом случае для доказательства прямым способом ложности частного положения необходимо доказать истинность противоречащего ему общего положения, другими словами, доказать, что «ни один язык не является надстройкой».
Но опровержение может быть и косвенным. Оно совершается посредством уже известного нам приёма «приведения к нелепости» (reductio ad absurdum). Получение нелепого заключения путём вывода, все основания которого, кроме одного, заведомо истинны, и есть косвенное опровержение, т. е. косвенное доказательство посредством закона противоречия ложности того единственного основания, относительно которого не было известно, истинно оно или ложно, и которое только предполагалось истинным.
3. Различие доказательств по роли опытных данных как оснований доказательства
Во всех науках и во всех научных доказательствах все понятия, которые входят в состав доказательства, ведут своё происхождение в конечном счёте из материальной практики, из опыта. В этом отношении не составляют исключения и доказательства математических наук. Правда, понятия, которыми пользуется математик, отвлекаются от целого ряда свойств, принадлежащих предметам этих понятий. Математический круг, куб, шар и т. д. не существуют в опыте в том виде, в каком их мыслит ум геометра. И всё же даже самые отвлечённые понятия математики возникли в конечном счёте из опыта и на основе опыта. Это справедливо и относительно математических определений и относительно аксиом, т. е. недоказываемых положений, принадлежащих к начальным основаниям всего математического знания. Какими бы далёкими от опыта, а иногда даже противоречащими опыту ни казались эти определения и аксиомы,— все они в конце концов являются продуктами отвлечения от известных сторон опыта и не могли сложиться в мысли иначе, как на основе опыта.
Идеалисты отрицают опытное происхождение математических понятий. При этом они опираются на то, что математика мыслит свои предметы — линии, поверхности, тела и т. д.— такими, какими они в точности никогда не бывают в действительности. Математическая линия, например, имеет лишь длину, но не имеет ни ширины, ни высоты, математическое тело есть лишь замкнутая математическими поверхностями часть пространства, мыслимая независимо от наполняющего пространство вещества, и т. д. Опираясь на эту отвлечённость современных математических понятий, идеалисты утверждают, будто понятия эти не могут иметь своим источником опыт и потому являются априорными, т. е. внеопытными и доопытными.
Так, идеалист Кант утверждает, будто «настоящие математические положения всегда суть априорные, а не эмпирические суждения, потому что они обладают необходимостью, которая не может быть заимствована из опыта»[25].
И точно так же идеалист-неокантианец Эрнст Кассирер утверждает, будто тенденция современной науки «всё более и более ведёт к тому, что устраняются «данные» элементы, как таковые, и им не уделяется никакого влияния на общую форму хода доказательства»[26]. «Всякое понятие и всякое положение, которое употребляется в ходе доказательства и не служит просто для целей наглядности, должно быть обосновано строго и выведено целиком из законов конструктивной связи»[27].
Выражаясь проще, математическое понятие есть, согласно взгляду идеалистов, не порождение опыта, а порождение (или построение, «конструкция») ума, отливающееся в априорные формы мысли и возникающее по априорным законам мышления.
Учение идеализма о внеопытном и доопытном характере математических понятий совершенно ошибочно. Несостоятельность этого учения была доказана Энгельсом в «Анти-Дюринге». Исходя из того же самого факта — крайней обобщённости и отвлечённости математических понятий,— на котором идеализм всегда строил свою философию математики, Энгельс показал, что правильным объяснением этого факта может быть только материалистическое. «Понятие фигуры, как и понятие числа,— разъяснял Энгельс,— заимствовано исключительно из внешнего мира, а не возникло вовсе в голове из чистого мышления. Раньше чем люди могли прийти к понятию фигуры, должны были существовать вещи, которые имели форму и формы которых сравнивали. Чистая математика имеет своим предметом пространственные формы и количественные отношения действительного мира, т. е. весьма реальное содержание. Тот факт, что это содержание проявляется в крайне абстрактной форме, может лишь слабо затушевать его происхождение из внешнего мира. Чтобы изучить эти формы и отношения в их чистом виде, следует их оторвать совершенно от их содержания, устранить его как нечто безразличное для дела. Так получаются точки без протяжения, линии без толщины и ширины, а и Ь, х и у, постоянные и переменные. ..Точно так же выведение математических величин как будто бы друг из друга доказывает не их априорное происхождение, но только их рациональную связь. Прежде чем пришли к мысли выводить форму цилиндра из вращения прямоугольника вокруг одной из его сторон, нужно было исследовать не мало реальных прямоугольников и цилиндров, хотя бы и в весьма несовершенной форме... как и во всех областях мышления, отвлеченные от действительного мира законы на известной ступени развития отрываются от действительного мира, противопоставляются ему как нечто самостоятельное, как явившиеся извне законы, по которым должен направляться мир... так, а не иначе, применяется впоследствии чистая математика к миру, хотя она и заимствована из этого мира и представляет только часть его составных форм несобственно, только поэтому она вообще применима к нему»[28].
Так обстоит дело с понятиями, определениями и аксиомами математики. Сложнее обстоит дело с доказательствами. Во всех науках, кроме математических, доказательство всегда непосредственно связано с опытом. Это значит, что кроме той связи с опытом, без которой вообще не могло бы существовать никакое понятие, никакая аксиома, в науках этих в состав доказательства всегда входят такие части и такие данные, которые прямо предполагают обращение к опыту: к наблюдению, эксперименту и т. д.
Напротив, в математических науках доказательства (если рассматривать одну логическую их сторону, а не происхождение понятий, входящих в состав доказательств) всегда ведутся таким образом, что в ходе доказательства математику не приходится прямо обращаться к опыту, помимо тех обобщений опыта, которые уже содержатся в его понятиях, определениях и аксиомах. Иными словами, опыт входит в математические доказательства не непосредственно, как он входит в доказательства физика, химика, биолога, но лишь посредством понятий, которые образуются на основе опыта, но в своём содержании являются отвлечёнными по отношению к этому опыту.
Это различие между науками математическими и науками эмпирическими, т. е. доказывающими свои положения при участии прямого обращения к опыту, порождает различие в видах доказательства.
Доказательства математических наук, не требующие привлечения прямых данных опыта в самом ходе доказательства и опирающиеся на опыт лишь через посредство тех обобщений опыта, которые содержатся в основных понятиях, определениях и аксиомах этих наук, называются математическими доказательствами.
Доказательства наук, необходимо требующие привлечения прямых данных опыта в самом ходе доказательства и, таким образом, не ограничивающиеся теми обобщениями опыта, которые содержатся в их основных понятиях, называются эмпирическими доказательствами.
Из этих определений и объяснений ясно, что различие между двумя рассматриваемыми видами доказательства состоит вовсе не в том, что доказательства математических наук стоят якобы вне опыта, а доказательства эмпирических наук основываются на опыте. Все доказательства всех наук — математических так же, как и эмпирических,— предполагают опыт в качестве необходимой и последней основы и в качестве критерия истинности всех своих положений.
Различие между этими двумя видами доказательства обусловлено только тем, что в одном случае самим ходом доказательства требуется прямое обращение к данным опыта, в другом же для осуществления доказательства достаточно той связи с опытом, которая дана уже в содержании понятий, входящих в состав доказательства. Из сказанного видно, что различие между математическими и эмпирическими доказательствами — не безусловно. Об этом свидетельствует также и следующее. Ряд наук о природе, доказывающих свои истины при помощи прямого обращения копыту, содержит в себе и такие части, в которых доказательства ведутся по методу математических наук. С другой стороны, и в математических науках математической форме доказательства часто предшествует обоснование, предполагающее прямое обращение к опыту, так что математическая форма доказательства вырабатывается впоследствии уже после того, как истинность доказываемого тезиса стала известной из опыта. Примером такого перехода от найденного в опыте результата к его математическому и дедуктивному по форме обоснованию может быть история определения Архимедом площади параболы.
VI. Ошибки в доказательствах
Как и всякое логическое действие, доказательство может быть правильным или ошибочным.
Первым необходимым условием правильности доказательства является истинность доказываемого тезиса по существу его содержания. В логическом строении доказательства тезис играет роль следствия, а аргументы и демонстрация — роль основания. Так как ложность следствия всегда означает ложность основания, то при условии, если доказываемый тезис ложен, всякое доказательство этого тезиса — каким бы ни был способ самого доказательства — всегда может быть только ложным. При этом ложность доказательства может быть троякая.
Во-первых, ошибка может состоять в том, что доказываемый тезис ошибочно отождествляется с другим — истинным — тезисом. В этом случае доказательство истинного тезиса может быть вполне правильным, а ошибка состоит в том, что правильное доказательство этого другого — истинного — тезиса принимается за доказательство того ложного тезиса, который хотели доказать и с которым ошибочно отождествили доказанный истинный тезис. Ошибка этого рода называется «подменой доказываемого тезиса» (её латинское название — ignoratio elenchi).
Во-вторых, ошибка может состоять в том, что доказываемый тезис выводится из ложных или из недоказанных и потому сомнительных аргументов. В этом случае демонстрация может быть логически последовательной, тезис может логически следовать из принятых аргументов, но в то же время может оказаться ложным по существу своего содержания. Ошибка этого рода называется «ошибкой ложного или сомнительного основания».
В-третьих, ошибка может состоять в том, что доказываемый тезис выводится из истинных аргументов, однако самый способ выведения, или демонстрация,— неправильный, логически ошибочный, так что доказываемый ложный тезис выводится только в силу ошибки, допущенной в ходе демонстрации. Этот вид ошибки называется «ошибкой в демонстрации, или в способе доказательства».
Само собой разумеется, порочность доказательства может быть обусловлена и соединением указанных ошибок. Например, ложность оснований может сочетаться с ошибкой в демонстрации.
Рассмотрим последовательно все три вида ошибок, возможных в доказательстве.
1. Подмена доказываемого тезиса
Ошибка подмены тезиса другим — истинным, правильно доказанным, но не тождественным с тем, который должен быть доказан, встречается очень часто. Опасность этой ошибки очевидна. Она состоит в том, что, следя за доказательством и видя, что аргументы — истинны, демонстрация — правильная, тезис — логически следует из оснований, мы можем не заметить подмены тезиса. Нам кажется, что правильно доказанный тезис и есть тот тезис, который должен быть доказан, в то время как в действительности тезисы эти — не тождественные. Но если тезисы не тождественны, то истинность и правильность доказательства одного вовсе не означает истинности и правильности доказательства другого.
Логическая суть ошибки подмены доказываемого тезиса состоит в нарушении закона тождества — в отождествлении различного, нетождественного.
Примером ошибки подмены доказываемого тезиса может быть вскрытая В. И. Лениным ошибка в рассуждении теоретика «экономизма» Мартынова. Последний хотел доказать, будто революционная партия рабочего класса не может руководить активной деятельностью различных революционно настроенных слоёв. Однако вместо доказательства этого — ложного, ошибочного, вредного — положения, Мартынов доказал другое положение. Он доказал, что в предреволюционный период различные общественные слои идут к решению задачи низвержения самодержавия «вразброд».
Ошибка Мартынова состояла в том, что доказательство этого последнего положения он принимал и выдавал за доказательство первого положения. Но положения эти — не тождественны, различны, а потому доказательство Мартынова оказалось логически ошибочным, свелось к подмене доказываемого тезиса.
И действительно: Мартынов доказывал— и в этом он был прав,— что революционная партия не могла в предреволюционный период руководить борьбой различных общественных групп за их ближайшие — слишком различные — профессиональные интересы.
Но вместе с тем Мартынов ошибочно думал, будто его рассуждение доказало, что революционная партия рабочего класса не может руководить революционной борьбой различных общественных групп, т. е. борьбой уже не за ближайшие и не за различные для каждой группы интересы, а борьбой политической, борьбой за низвержение самодержавия, борьбой, которая в то время уже объединяла различные революционно настроенные группы и которая требовала руководства со стороны передовой революционной партии.«...Начав говорить о революционной энергии,— писал Ленин,— об активной борьбе за низвержение самодержавия, Мартынов сейчас же сбился на профессиональную энергию, на активную борьбу за ближайшие интересы! Понятно само собой, что мы не можем руководить борьбой студентов, либералов и проч. за их «ближайшие интересы», но ведь не об этом же была речь, почтеннейший экономист! Речь шла о возможном и необходимом участии разных общественных слоев в низвержении самодержавия, а этой «активной деятельностью разных оппозиционных слоев» мы не только можем, но и непременно должны руководить, если мы хотим быть «авангардом»»[29].
Подмена тезиса возможна не только в простом доказательстве, но и в опровержении. Так бывает, когда, взявшись опровергнуть одно положение, вместо него опровергают другое, о котором думают, однако, будто оно и есть то самое положение, которое взялись опровергнуть. Разумеется, и здесь суть ошибки—в нарушении закона тождества, в отождествлении различного и нетождественного. Так бывает, например, когда, опровергнув способ доказательства, посредством которого противник пытался обосновать свой тезис, ошибочно полагают, будто тем самым опровергли и самый доказываемый тезис по существу его содержания.
Совершенно очевидно, что в этом случае произошла подмена опровергаемого тезиса другим тезисом: взялись опровергнуть самый тезис, а опровергли только способ его доказательства. Но это — не одно и то же! Опровержение способа доказательства не есть ещё опровержение доказываемого тезиса. Возможно, что способ доказательства — неправильный, ошибочный, а доказываемое положение — само по себе, по существу своего содержания — истинно. Тогда задача заключается не в том, чтобы опровергнуть тезис, а в том, чтобы исправить способ доказательства, заменить ошибочное доказательство правильным.
Во всех случаях подмены доказываемого тезиса логическая сущность этой ошибки остаётся той же самой. Это — ошибочное отождествление доказанного тезиса, о котором в доказательстве не было и речи, с тем тезисом, который должен быть доказан. Поэтому о логической стороне ошибки подмены доказываемого тезиса в сущности нечего прибавить к тому, что уже сказано.
Однако в вопросе об этой ошибке есть другая важная сторона — не логическая. Дело в том, что возникает законный вопрос: каким образом, при каких условиях может произойти отождествление различных тезисов: доказанного, но не относящегося к делу, с тем, который должен быть доказан?
Ответ на этот вопрос имеет несомненное практическое значение. Знание обстоятельств, при которых в доказательстве легко может возникнуть логическая ошибка, способствует предупреждению самой ошибки.
Ошибка подмены доказываемого тезиса всего легче возникает там, где тезис, доказанный вместо того тезиса, который должен быть доказан, создаёт предубеждение или склонность к тому, чтобы считать доказанным и этот второй тезис. Предубеждение это способствует отождествлению различных тезисов и ослабляет внимание к тому, в чём они различны.
Одним из наиболее сильно действующих в этом направлении приёмов является приём, при котором оценка дела подменяется оценкой известных — положительных или отрицательных — качеств лица, совершившего или совершающего это дело. Приём этот основывается на том, что известные из прошлого или из настоящего опыта качества лица могут в известных случаях предопределять и качество совершаемого лицом дела. Так, если о человеке N известно, что он крайне нерешителен, медлителен и склонен к колебаниям, то можно с известной долей вероятности предполагать, что это качество тот же человек проявит и в новом поручаемом ему деле, требующем решительного, твёрдого и быстрого образа действий.
Однако предположение это остаётся лишь более или менее вероятным. К тому же в ряде случаев связь между известным из опыта нравственным характером лица и совершаемым им делом — далеко не непреложная. Поэтому с логической точки зрения для заключения от известных качеств лица к оценке конкретного дела, совершаемого этим липом, разумеется нет достаточного основания.
Несмотря на полную логическую недопустимость подобных заключений, их делают очень часто. Оценку дела подменяют оценкой лица. Психологическое или моральное впечатление от качеств лица переносят на оценку, например, теории, которую это лицо развивает, или на положение, которое этим лицом доказывается.
С логической точки зрения ошибка эта — та же ошибка подмены доказываемого тезиса. Но ввиду особого значения, которое имеет указанное происхождение этой ошибки, она получила особое название — «довода от человека»[30].
Пример ошибки довода от человека представляет разоблачённая Лениным ошибка Каутского, сделанная последним в споре о тактике социал-демократии во время империалистической войны. Большевики справедливо обвиняли некоторых видных деятелей западной и русской социал-демократии — Вальяна, Геда, Гайндмана и Плеханова — в переходе на сторону «своих» империалистических правительств в вопросе о войне. Каутский пытался защищать этих социал-демократов при помощи следующего довода: «...кто захотел бы серьезно утверждать, — писал Каутский,— что такие люди, как Вальян и Гед, Гайндман и Плеханов, в один день сделались империалистами и предали социализм?»[31].
Это рассуждение Каутского — типичный случай логической ошибки довода от человека. Вместо того чтобы доказать, что Вальян, Гед, Гайндман и Плеханов в этом случае, в данном вопросе не предали социализм и не стали на сторону империалистов, Каутский доказывает, что они — такие люди, которые по своим качествам, хорошо известным из их прошлой деятельности, вообще не могли этого сделать.
На основании заслуг этих людей — заслуг, которые относятся только к их действиям в прошлом, Каутский считает доказанным, будто и в настоящем вопросе они являются верными социализму борцами за интересы рабочего класса.
Среди советских работников в области общественных наук долгое время имело хождение осуждённое партией догматическое, начётническое отношение к марксизму-ленинизму. Некоторые товарищи вместо того, чтобы доказывать то или иное положение, опираясь на данные опыта, практики, считали достаточным сослаться на отдельные высказывания классиков марксизма-ленинизма, по большей части выхваченные из контекста, оторванные от контекста. Эти научные работники полагали, будто уже тот факт, что цитата взята из произведения классика марксизма-ленинизма, великого корифея науки, вождя и учителя трудящихся, сам по себе является доказательством истинности этой цитаты, принимаемой в качестве основания доказываемого тезиса.
Классики марксизма-ленинизма всегда выступали против такого суеверного отношения к личности (хотя бы и к великой личности) и к её отдельным высказываниям. Партия требует от коммунистов, а также и от всех работников науки творческого изучения действительности. При этом, конечно, необходимо руководствоваться марксистско-ленинской теорией. Однако исходить нужно не из отдельных формулировок и цитат, а из существа марксизма-ленинизма. В тезисах отдела пропаганды и агитации ЦК КПСС и Института Маркса — Энгельса — Ленина — Сталина при ЦК КПСС, опубликованных в связи с 50-летием Коммунистической партии Советского Союза, говорится: «Исходя из того, что марксистско-ленинская теория есть не догма, а руководство к действию, партия требует от коммунистов понимания творческого характера марксизма-ленинизма, усвоения не отдельных формулировок и цитат, а действительного существа всепобеждающего, преобразующего мир революционного учения Маркса — Энгельса — Ленина — Сталина»[32].
Довод от человека чаще всего представляет собой не невольную логическую ошибку, а намеренный софистический приём. Довод этот рассчитан не столько на логическую рассудительность, сколько на способность людей поддаваться чувству и переносить оценки, сложившиеся под влиянием чувства, на предметы и действия, не имеющие никакого отношения к тому, чем эти чувства были вызваны.
Приём этот лучше всего удаётся в отношении людей, у которых чувство берёт верх над логикой. Чем ниже у человека уровень логической культуры, чем слабее логический контроль и самоконтроль, тем легче способен такой человек отождествить доказанный и сильно действующий на его чувства тезис с другим тезисом, который должен быть доказан, который не доказан, но который кажется ему вытекающим из первого.
Поэтому для того, чтобы не поддаться действию довода от человека, необходимо рассматривать только логическую силу доказательства, отвлекаясь от всех соображений, кроме тех, которые относятся к обоснованности, т. е. истинности, оснований и к логической правильности доказательства. Необходимо сохранить полное самообладание и, прослеживая ход доказательства, не дать своим чувствам увлечь себя настолько, чтобы не заметить подмены доказываемого тезиса другим. В этом смысле Ленин писал в статье «Должны ли мы организовать революцию?»: «...мы желали бы, чтобы чувство радости по поводу возможных приятностей не затемняло нашей логики»[33].
2. Ошибки в основаниях доказательства
Истинность доказываемого (или ложность опровергаемого) тезиса — первое необходимое условие логической безупречности доказательства. Но это условие — не единственное. В безупречном доказательстве истинный тезис выводится не из любых оснований, но только из оснований истинных. Поэтому вторым необходимым условием логической безупречности доказательства является истинность оснований, на которые опирается доказательство. Так как из истинности основания всегда вытекает истинность следствия, то при условии, если демонстрация ведётся правильно, следствие, т. е. доказываемый тезис, также будет истинным.
Напротив, при ложности основания следствие может оказаться как истинным, так и ложным. При этом вопрос о том, будет ли следствие истинным или ложным, остаётся совершенно открытым даже при условии, если демонстрация вполне безупречна, т. е. если доказываемый тезис действительно логически следует из принятых оснований.
Требованиям доказательства не удовлетворяют основания не только явно ложные, но и сомнительные, недоказанные. И в том и в другом случае вопрос об истинности доказываемого тезиса остаётся открытым. И в том и в другом случае доказательство не достигает своей цели — не даёт определённого ответа на вопрос, истинен или ложен доказываемый тезис.
Совершенно очевидно, что при указанных условиях доказательство будет логически ошибочным. Доказательство, приводящее к тезису, относительно которого неизвестно, истинен он или ложен,— негодное доказательство.
а) Ошибка ложного основания
Первым видом ошибок в основаниях доказательства является ошибка ложного основания. Она состоит в том, что в качестве основания используется ложное положение, которое, однако, считают истинным или выдают за истинное. Рассматривая взятое ложное основание в качестве истинного, развивают далее правильную демонстрацию, которая приводит, как к заключению, к доказываемому тезису.
Ошибка ложного основания, как и всякая логическая ошибка, может быть либо непреднамеренным, непроизвольным заблуждением, либо сознательно применяемым приёмом, т. е. софизмом.
Непреднамеренная ошибка ложного основания возникает, во-первых, вследствие незнания того, что положение, принятое в качестве основания, ложно. Ошибка эта встречается очень часто. Многие положения, которые в течение долгого времени считались истинными и несомненными, оказались впоследствии ложными. А между тем эти ложные положения до установления их ложности использовались и используются в качестве оснований во многих доказательствах, приводили и приводят во многих случаях к ложным заключениям.
Так, в течение тысячелетий считалось истиной положение о неподвижности земли.
Ещё недавно, до открытия О. Б. Лепешинской, многие биологи считали истинным ложное положение Вирхова о том, что органическая жизнь может вести начало только из клетки: omne vivum ex cellula. На этом и подобных ложных основаниях строились доказательства тезисов, которые оказались такими же ложными, как и их основания. На ложном положении о клетке как единственном источнике жизни строились ложные заключения о вечности органических форм, о невозможности превращения вещества, не имеющего клеточного строения, в вещество органическое и т. д.
Во-вторых, непреднамеренная ошибка ложного основания часто возникает вследствие неправильного отождествления различных оснований. А именно: не редки случаи, когда в качестве основания берут положение, истинное только при известных условиях или в известном ограниченном смысле, в строго определенном отношении. При этом, однако, положение это рассматривают как истинное безусловно, без всяких ограничений, безотносительно. Но в этом безусловном смысле оно может оказаться ложным. Совершенно очевидно, что здесь происходит подмена, отождествление различных положений. Взяв в качестве основания положение, истолкованное в безотносительном смысле и в этом смысле ложное, приходят в результате доказательства к ложному заключению.
Примером этой ошибки может быть высмеянное В. И. Лениным рассуждение реакционного буржуазного экономиста и философа С. Н. Булгакова. Этот экономист хотел доказать, будто увеличение числа и площади крупных земледельческих хозяйств ведёт к упадку сельского хозяйства. В качестве основания он указывал на то, что при известных условиях уменьшение площади хозяйства приводит к увеличению его продуктивности.
«Видите,— писал по поводу этого доказательства Ленин,— как замечательно логично рассуждает наш «ученый»: так как уменьшение площади хозяйства означает иногда, при интенсификации, рост производства, поэтому увеличение числа и площади латифундий должно вообще означать упадок!»[34]. В этом «доказательстве» Булгакова основание, истинное только при определённых ограниченных условиях, принято в качестве истинного безусловно. А так как в таком безусловном содержании основание это ложно, то и опирающееся на него заключение (положение об упадке, неизбежном будто бы для крупных хозяйств) оказалось ложным.
Специальное название этой ошибки — ошибочный вывод от сказанного под известным условием к сказанному безусловно (fallacia a dicto secundum quid ad dictum simplicitor).
Преднамеренная ошибка ложного основания возникает тогда, когда желают доказать во что бы то ни стало заведомо ложный тезис. Так как в этом случае никакой правильный способ доказательства не может привести к цели (ибо ложный тезис не может быть доказан), то остаётся только один путь — выводить тезис из заведомо ложного основания, однако из такого основания, из которого требуемый тезис выводится как логическое следствие. А так как из ложного основания может быть получено как истинное, так и ложное следствие, то, для того чтобы скрыть это обстоятельство, софист прибегает к уловке: он или догматически провозглашает взятое им ложное основание истинным, или же объявляет, будто истинное под известным условием основание истинно безусловно, а затем уже выводит из подменённого таким образом основания требуемое следствие, т. е. доказываемый тезис.
Совершенно очевидно, что с логической точки зрения ошибка ложного основания остаётся той же самой независимо от того, намеренно или ненамеренно она допускается в доказательстве. Но практически очень важно и полезно знать, посредством каких уловок ошибочное доказательство может быть выдано за правильное.
Опасность доказательства, применяющего ложное основание, состоит в том, что для тех, кто не знает о ложности основания, доказательство кажется безупречным: демонстрация в таком доказательстве может быть правильной, а тезис может логически вытекать из принятых оснований.
Опровержение такого доказательства сводится, очевидно, к опровержению основания, т. е. к доказательству его ложности. Как всякое опровержение, опровержение ложного основания может быть либо прямым, либо косвенным. Прямое опровержение состоит в отыскании и в указании фактов или положений, о которых известно, что они истинны, и которые противоположны опровергаемому основанию. Так, мнимые доказательства последователей теории Вирхова, основывающейся на утверждении, что «всё живое — только из клетки», оказались опровергнутыми, когда О. Б. Лепешинская доказала своими опытами, что существует живая материя, не имеющая клеточного строения.
Косвенное опровержение ложного основания состоит в доказательстве того, что существует следствие, необходимо вытекающее из этого основания и противоречащее какому-нибудь известному и заведомо истинному положению. Оказавшись — согласно закону противоречия — ложным, следствие это, как ложное следствие принятого основания, доказывает ложность самого основания.
Ошибка в основании, опровергаемая косвенным способом, имеет интересную особенность. Такое основание, очевидно, приводит к двум следствиям. Из него, во-первых, вытекает доказываемый тезис. Во-вторых, из него вытекает ещё некоторое следствие,противоречащее имеющемуся достоверному знанию. Другими словами, такое основание доказывает слишком много: не только доказываемый тезис, но и ещё некоторое положение, которое, однако, оказывается ложным.
Так как всякое основание, приводящее к такому результату, ложно, то отсюда получается следующее правило: «кто слишком много доказывает, тот ничего не доказывает» (qui nimium probat nil probat). Ошибка этого рода называется ошибкой «чрезмерного доказательства».
Пример ошибки чрезмерного доказательства представляет рассуждение, с которым выступил в ноябре 1948 г. в Организации Объединённых Наций бельгийский представитель. Он хотел доказать тезис о «неприемлемости» советских предложений о сокращении вооружений и вооружённых сил. Для доказательства этого тезиса он ссылался как на довод на тот факт, что при существующих международных отношениях не может быть общественного доверия к информации о выполнении предложенного Советским Союзом сокращения вооружённых сил и вооружений.
А. Я. Вышинский разъяснил в своей речи в ООН 11 ноября 1948 г., что это рассуждение бельгийского представителя доказывало «слишком много» и потому ничего не доказывало. Из довода об отсутствии — при существующих международных отношениях — общественного доверия к информации о ходе разоружения получался неизбежный вывод, что — при этих условиях — не может быть также доверия и к информации о современном состоянии вооружённых сил,— информации, которую предложил французский представитель и за которую ратовал представитель Бельгии. Другими словами, из аргумента бельгийского представителя вытекал не только тот тезис, который он взялся доказать, но, кроме того, вытекал и некоторый дополнительный тезис, который сам же бельгийский представитель считал абсурдным.
Обычно источником ошибки чрезмерного доказательства является стремление получить вывод непременно из общих посылок. Так как из истинности общего положения следует истинность подчинённого ему частного положения, то, приняв некоторое общее положение в качестве истинного, легко получить из него искомый вывод. Но если взятая в столь общем виде посылка ложна, то ложность её непременно должна быть обнаружена, как только будет установлено, что следствие, необходимо вытекающее из этой посылки, противоречит известным истинным фактам или истинным положениям.
Не следует думать, будто всякое основание, из которого, кроме доказываемого тезиса, необходимо вытекает ещё некоторое дополнительное следствие, непременно будет ложным. Ложным оно будет только в том случае, если дополнительно выведенное из него следствие стоит в противоречии с имеющимся знанием. Но если следствие, выведенное из основания и дополнительное по отношению к доказываемому тезису,— истинно, то доказательство, опирающееся на такое основание, будет правильным.
б) Ошибка недоказанного основания
Вторым видом ошибки в основаниях доказательства является ошибка недоказанного основания.
Так как только истинное основание ведёт всегда и необходимо к истинному заключению и так как доказываемый тезис необходимо должен быть истинным, то основание, из которого этот тезис выводится, должно быть непременно истинным. Но истинность основания в подавляющем большинстве случаев неочевидна. Только немногие положения, используемые в качестве оснований доказательства, обладают «очевидностью». К тому же «очевидность» всегда заключает в себе момент субъективный: что кажется вполне очевидным одному, часто представляется далеко не очевидным другому. Поэтому во всех доказательствах все неочевидные основания должны быть доказанными основаниями. Недоказанное основание — с логической точки зрения — не есть основание, а доказательство, опирающееся на такое основание,— ошибочное доказательство.
Латинское название ошибки недоказанного основания— petitio principii, т. е. «предвосхищение основания». Название это показывает, что положение, использованное в доказательстве в качестве основания, будучи недоказанным, только предвосхищает основание, но на деле не обосновывает заключения и потому не является основанием.
Примером логической ошибки petitio principii может быть «доказательство», посредством которого реакционный английский экономист Мальтус пытался защитить социальные основы имущественного неравенства в современном ему капиталистическом обществе, а также доказать бессилие всех попыток, направленных к устранению этого неравенства. Мальтус хотел доказать, что в то время как численность населения возрастает в геометрической прогрессии, производительность земли, дающей населению средства существования, возрастает только в арифметической прогрессии. При этом в качестве основания для доказательства того, что население удваивается в течение 25 лет, Мальтус использовал статистические данные, согласно которым именно таков был в течение долгого периода прирост населения в США.
Однако основание, использованное Мальтусом, было основанием недоказанным. Мальтус взял числовой итог статистики и не проанализировал, из каких составных частей он слагается и можно ли весь этот итог отнести за счёт естественного прироста коренного народонаселения.
Ошибку petitio principii в доказательстве Мальтуса вскрыл Н. Г. Чернышевский в «Замечаниях» к «Основаниям политической экономии» Дж. С. Милля. «Читатель видит,— писал Чернышевский,— на чём оперлась мысль Мальтуса, когда он положил, что население может удвоиваться в 25 лет: в Северо-Американских Штатах оно очень долго удвоивалось по таким срокам. Просим посмотреть, вспомнилось ли ему тут, что за всё это время увеличению числа людей в Соединённых Штатах содействовало переселение туда людей из Европы? Нет, он не вспомнил этого, когда составлял свою теорию»[35]. «Из этого,— продолжает Чернышевский,— мы можем заключить, много ли критики, много ли осмотрительности было у него, когда он определял одно из оснований для своего вывода... основание для вывода принято без всякой критики...»[36]
Ту же ошибку — petitio principii — Мальтус делает, когда доказывает отставание роста производительности земли от роста народонаселения. Мальтус принимает за основание положение, будто производительность земли может возрастать только в арифметической прогрессии. Но это основание во времена Мальтуса было недоказанным, а впоследствии оказалось просто ложным.
Ошибка недоказанного основания имеет разновидность, заслуживающую особого рассмотрения. В некоторых доказательствах недоказанность основания выступает в замаскированной форме, а именно: основание доказывается, однако доказывается при помощи того самого тезиса, который должен быть доказан. Так как тезис этот ещё не доказан, то положение, выведенное с его помощью, тоже не может считаться доказанным. А так как в данном случае положение это выступает в роли основания, то мы имеем здесь ошибку недоказанного основания.
Ошибка, состоящая в том, что в доказательстве в качестве основания используется положение, доказанное с помощью самого доказываемого тезиса, называется «кругом в доказательстве», «ложным кругом», «порочным кругом». Латинское название этой ошибки — circulus in demonstrando.
Круг в доказательстве легко может быть замечен, если рассуждение коротко и несложно. Но в доказательствах, состоящих из длинных цепей умозаключений, круг может остаться незамеченным.
Примером круга в доказательстве может быть доказательство конечности и ограниченности вселенной, применявшееся противниками учения Коперника о движении Земли и планет солнечной системы вокруг Солнца. Противники Коперника доказывали конечность вселенной, опираясь, как на основание, на утверждение, будто вселенная совершает в течение суток полный оборот вокруг неподвижного центра, совпадающего с центром Земли. В свою очередь истинность этого основания они доказывали, опираясь на конечность вселенной, так как при условии её бесконечности нельзя понять, каким образом бесконечная вселенная могла бы в течение одних суток совершить полный оборот около своего центра. Другими словами, тезис (положение о конечности мира) доказывался посредством основания (суточное вращение мира вокруг центра), основание же это само доказывалось при помощи доказываемого тезиса.
3. Ошибки в демонстрации, или в способе доказательства
Кроме ошибки подмены доказываемого тезиса и ошибок в основаниях, в доказательстве возможен ещё третий вид ошибок. Это — ошибки в демонстрации, т. е. в способе, посредством которого совершается логический переход от принятых оснований к доказываемому тезису. Сами по себе ни тезис, ни основания (хотя бы они были истинны) ещё не составляют доказательства. Доказательство имеет место только там, где истинный тезис выводится из принятых истинных оснований, другими словами, где показывается, что нельзя, признав основания истинными, не признать истинным и тезис.
Отсюда видно, что демонстрация есть способ выяснения логической связи между основаниями доказательства и самим доказываемым тезисом. Будучи способом выяснения логической связи между основаниями и тезисом, демонстрация должна быть логически безупречной. Это значит, что истинность доказываемого тезиса действительно должна вытекать из истинности принятых оснований.
Поэтому всякий способ доказательства, не достигающий этой цели, т. е. не приводящий от признания истинности оснований к истинности доказываемого с их помощью тезиса, будет логически ошибочным.
Всякая ошибка в демонстрации так или иначе сводится к отсутствию действительной логической связи между основаниями и доказываемым тезисом. При этом возможны два случая.
Первый случай, или первый вид, ошибки в демонстрации состоит в том, что демонстрация, сама по себе логически правильная, не имеет, однако, никакого отношения к доказываемому тезису. Это значит, что тезис просто механически присоединяется к демонстрации, но не является её логическим результатом. В таких случаях говорят, что тезис не следует из оснований, а сама ошибка такого доказательства обозначается латинским термином поп sequitur (т. е. «не следует»).
Ошибка поп sequitur встречается гораздо чаще, чем можно предполагать. Многие люди наивно думают, что если между любым рассуждением, хотя бы оно вовсе не относилось к делу, и доказываемым тезисом они поставят союз «следовательно», «стало быть», «итак» и т. п., то между этим их рассуждением и доказываемым тезисом будет установлена необходимая логическая связь. Отсутствующую логическую связь они заменяют тем словом, которым эта связь (там, где она существует) выражается в языке. Им кажется, что, вставив между рассуждением и выводом слово «следовательно», они тем самым сообщают своему рассуждению ту логическую необходимость, которую имеет не слово само по себе, но только слово, выражающее действительно логическую связь.
Ошибка эта часто встречается в мышлении людей небрежных, не способных сосредоточенно следить за логической связью мыслей в чужих и в собственных рассуждениях. Ещё чаще она встречается в рассуждениях людей, которые, стремясь во что бы то ни стало доказать тезис, представляющийся им очень важным и являющийся для них желательным, но не будучи в состоянии сделать это либо в силу ложности самого тезиса, либо в силу собственной логической беспомощности, подменяют логическую демонстрацию словесной видимостью демонстрации.
Примером ошибки поп sequitur может быть разоблачённая Лениным ошибка в резолюции ликвидаторской конференции 1912 г. В резолюции этой утверждалось, что нелегальные партийные организации должны приспособляться к новым формам и методам легального рабочего движения. Необходимость этого изменения ликвидаторы выводили из того, что общественно-политические условия в России после революции 1905 г. уже не те, что были до революции. «Ввиду изменения общественно-политических условий по сравнению с дореволюционной эпохой,— так гласил § 2 резолюции ликвидаторов,— существующие и вновь возникающие нелегальные партийные организации должны приспособляться к новым формам и методам открытого рабочего движения»[37].
Разбирая это доказательство, Ленин показал, что в нём тезис никак не следует из приведённых оснований. «Для чего,— спрашивает Ленин,— ссылается резолюция на «изменение общественно-политических условий»? Очевидно,— отвечает он,— для того, чтобы доказать, обосновать, вывести свой практический вывод: необходимо для нелегальной организации приспособляться к легальному движению. Но из посылки такой вывод отнюдь не вытекает»[38]. «Из изменения общественных условий,— пояснял Ленин,— вытекает лишь изменение формы организации, но направление этого изменения ничем в резолюции не обосновано»[39].
Разобранная Лениным ошибка — типичный случай ошибки поп sequitur. Ошибка здесь состоит в том, что из демонстрации выводится не то, что из неё действительно следует (не необходимость изменения форм организации), а то, что из неё никак не следуем (необходимость особого направления самого этого изменения: необходимость приспособления нелегальной организации к легальному движению). Тезис этот не вытекает логически как вывод из всей демонстрации, а механически присоединяется к демонстрации без всякой логической связи с нею. Присоединение это создаёт лишь видимость логической связи между основаниями и заключением.
В этом примере причина логической ошибки в том, что тезис о приспособлении нелегальной партии к легальному движению представлялся ликвидаторам истинным, а его осуществление — чрезвычайно важным. Желание во что бы то ни стало доказать этот безусловно ложный тезис привело ликвидаторов к тому, что они стали обосновывать его посылками, из которых он вовсе не следовал.
Ошибка поп sequitur — первый случай, или вид, ошибки в демонстрации.
Второй вид ошибки в демонстрации состоит в том, что в том или другом звене доказательства возникает какая-либо логическая ошибка, приводящая, однако, в соединении с другими звеньями доказательства к признанию истинности доказываемого тезиса. В этом случае доказываемый тезис может быть истинным, но всё доказательство в целом — ошибочно, так как демонстрация, связывающая основания с тезисом, заключает в своём развитии логическую ошибку.
При этом ошибки в демонстрации могут быть различного рода. Так как демонстрация представляет цепь умозаключений, ведущих от оснований к доказываемому тезису, то в демонстрации могут встречаться все ошибки, возможные в умозаключениях. Наиболее частыми из них являются следующие.
Так называется ошибка, состоящая в том, что некоторые посредствующие звенья демонстрации выпадают или остаются недоказанными. Ошибка чересчур поспешного вывода особенно часто встречается в доказательствах, где применяются индуктивные выводы (от частного к общему). Обобщение в этих случаях бывает слишком поспешным или при условии, если данные (факты, посылки), на которых основывается обобщение, недостаточны, неполны, или при условии, если, обобщая, игнорируют случаи, противоречащие общему выводу. Обычно оба эти недостатка тесно связаны: недостаточность данных приводит к тому, что случаи, противоречащие обобщению, остаются незамеченными, неучтёнными.
Распространённость этой ошибки отметил К. А. Тимирязев. Обычная, по его замечанию, ошибка старых геологов состояла в том, что о развитии всего органического мира они были склонны поспешно заключать на основании чрезвычайно недостаточных данных: «...Большинство геологов,— пишет К. А. Тимирязев,— было склонно преувеличивать действительное значение имеющихся данных и на основании ничтожных отрывочных сведений, имеющих чисто местное значение, полагало возможным судить об истории всего органического мира»[40].
Пропуск посредствующих звеньев демонстрации возможен и в доказательствах, в которых применяется дедукция. Так как дедуктивные умозаключения часто облекаются в форму энтимем, то возможны случаи, когда за энтимему принимают умозаключение, в котором известные посылки пропущены не потому, что они хорошо известны и достоверны, а, напротив, потому, что они ещё не доказаны. В таком случае энтимема оказывается мнимой, а доказательство — ошибочным.
Общее латинское название всех видов ошибок чересчур поспешного вывода — saltus in concludendo («прыжок в заключении»).
Так называется ошибка, при которой в умозаключении, образующем демонстрацию доказательства, нет посредствующего понятия, так как термин, выражающий это понятие, в одной из посылок относится к одному предмету, имеет одно значение, а в другой — относится к другому предмету п имеет другое значение. Это значит, другими словами, что в умозаключении произошло «учетверение терминов» (quaternio terminorum): вместо трёх терминов (большего, меньшего и среднего) их оказалось четыре. Так как терминов четыре и так как среди них нет термина, который играл бы роль термина, посредствующего между большим и меньшим терминами, то не видная сама по себе связь между предметом большего и предметом меньшего термина, связь, которая должна была быть выяснена из отношения каждого из них к предмету среднего термина, так и остаётся невыясненной, а потому и заключение оказывается логически неоправданным.
Ошибка учетверения терминов выступает в двоякой форме. Первая из них есть ошибка неправильного словесного выражения мысли (fallacia secundum dictionem), вторая — ошибка самого мышления, не зависящая от словесного выражения мыслей (fallacia extra dictionem). Каждая из этих ошибок в свою очередь имеет разновидности, обусловленные различными способами происхождения ошибочного умозаключения.
Так называется ошибка, связанная со смешением различных значений одного и того же слова. Дело в том, что в каждом высокоразвитом и богатом языке имеется множество омонимов, т. е. одинаковых звуковых сочетаний, обозначающих не совсем одинаковые, а иногда и вовсе различные предметы.
Для доказательства не представляют никакой опасности те омонимы, значения которых явно отличаются друг от друга, относятся к предметам или явлениям, совершенно различным. Например, термин «склонение» имеет три значения: 1) грамматическое (изменение флексий имён по падежам), 2) физическое (отклонение магнитной стрелки компаса в зависимости от близости к магнитному полюсу), 3) астрономическое (угловое расстояние светила от небесного экватора). Так как все эти значения слишком различны и относятся к совершенно различным областям реальности и познания, то смешение или отождествление их, конечно, невероятно.
Но есть омонимы, у которых значения хотя и различны, хотя и относятся к различным предметам или явлениям, однако относятся к предметам и явлениям той же самой или близких областей. В этих случаях опасность смешения и учетверения терминов, прикрываемого однозвучностью словесного выражения, безусловно существует.
Яркий пример учетверения терминов, основанного на омонимии, представляет собой ошибка Плеханова в его рассуждениях о национализации помещичьих земель. На объединительном съезде РСДРП в 1906 г. между Плехановым и Лениным шёл спор по вопросу о национализации земли. Возражая против требования большевиков о национализации помещичьих земель, Плеханов выдвинул следующий довод. Национализация земли, считал он, была экономической основой московской Руси допетровской эпохи. Революция 1905 года, как и всякая другая революция, не содержит в себе гарантий от реставрации (т. е. от восстановления старого, дореволюционного порядка). Поэтому в интересах избежания реставрации следует особенно остерегаться именно национализации[41].
Из ленинского опровержения этого довода видно, что, с логической точки зрения, ошибкой рассуждения Плеханова является учетверение терминов, использующее омонимию, или смешение двух различных по содержанию исторических понятий в одном и том же слове «национализация».
«Поскольку в московской Руси была (или: если в московской Руси была) национализация земли,— разъяснял Ленин,— постольку экономической основой ее был азиатский способ производства. Между тем, в России со второй половины XIX века укрепился, а в XX веке стал уже безусловно преобладающим капиталистический способ производства. Что же остается,— спрашивает Ленин,— от довода Плеханова? Национализацию, основанную на азиатском способе производства, он смешал с национализацией, основанной на капиталистическом способе производства. Из-за тождества слов он просмотрел коренное различие экономических, именно производственных, отношений»[42]. «Но такая логика,— продолжает Ленин,— есть именно софизм, а не логика, или игра в слова, без анализа экономической основы явлений или экономического содержания понятий»[43].
Использование омонимии — излюбленный приём, применяемый реакционными политическими деятелями и дипломатами капиталистического лагеря для доказательства ложных положений. Доказывая тезисы, направленные против подлинного социализма, против подлинной демократии, против подлинной свободы печати, деятели эти основываются на учетверении терминов, на смешении различных понятий, мыслимых посредством таких слов, как «социализм», «демократия», «свобода печати». Когда продажная капиталистическая печать называет политический строй современных США или Англии «демократическим», то слово «демократия» понимается не в смысле демократии для трудящихся масс, угнетаемых капиталом, а в смысле «демократии» для верхушки класса капиталистов. Когда капиталистическая пресса называет режим печати в капиталистических странах режимом «свободы печати», то слова «свобода печати» понимаются не в смысле действительной, фактической свободы печати для трудящихся и эксплуатируемых, а в смысле только формальной (да и то донельзя урезанной) свободы, осуществление которой на деле доступно только для той же верхушки господствующего реакционного класса капиталистов.
Во всех подобных случаях обманное, софистическое доказательство пользуется омонимией, прикрывающей логическую ошибку учетверения терминов.
Для устранения и для разоблачения ошибки учетверения терминов необходимо точное определение всех понятий, входящих в демонстрацию в качестве терминов умозаключений.
Ошибка неправильного словесного выражения мысли может проистекать не только из омонимии, т. е. из двусмысленности слова. Двусмысленным или даже многосмысленным может оказаться также и предложение. В этой связи в демонстрации может возникнуть ошибка, называемая амфиболией. Примером двусмысленного предложения может быть 107-й афоризм древнегреческого философа Гераклита: Κακοί μάρτυρες avipamot3tv οφθαλμοί και ώτα βάρβαρους ψυΧα έΧοντων («плохие свидетели глаза и уши у людей, которые имеют грубые души»)[44]. Предложение, посредством которого выражен этот афоризм,— двусмысленно. Его можно понимать, во-первых, в том смысле, что глаза и уши (т. е. ощущения) — плохие свидетели для людей, так как люди имеют грубые души. Основывается возможность такого понимания на том, что придаточное предложение βάρβαρου ψυΧας έΧοντων может быть переведено: «так как они (т. е. люди) имеют грубые души».
Во-вторых, предложение, выражающее 107-й афоризм, можно понимать и в том смысле, что хотя глаза и уши (ощущения) способны давать истину, однако люди, у которых грубые души, превратно толкуют свидетельства внешних чувств. Понимание это основывается на том, что придаточное предложение βάρβαρους ψυΧας εΧοντων может быть переведено: «если они (т. е. люди) имеют грубые души».
Оба толкования афоризма ведут к совершенно различным пониманиям взглядов Гераклита на роль и ценность внешних чувств и ощущений для познания. Первое толкование — «плохие свидетели глаза и уши для людей, так как у них грубые души» — ведёт к взгляду, согласно которому Гераклит будто бы считал показания ощущений ложными. Второе — «плохие свидетели глаза и уши для людей, если у них грубые души» — ведёт ко взгляду, согласно которому Гераклит считал ложными не показания чувств вообще и не ощущения как таковые, но лишь показания чувств тех людей, у которых грубые души.
Двусмысленность афоризма Гераклита была использована теми историками философии, которые стремились истолковать учение Гераклита о познании в духе идеализма и рационализма, как отрицание ценности чувств для познания. Историки эти, например Паскаль[45], доказывали свой тезис, используя только что разъяснённую нами двусмысленность гераклитовского афоризма. Доказательство это представляет пример амфиболии.
Другой пример амфиболии — «доказательство» махистов, пытавшихся отрицать, что развитая ими теория познания идеалистична. Для опровержения этого обвинения махисты ссылались на рассуждения виднейших философов махистского направления, которые не раз заявляли, что всё познание основывается на опыте, имеет источником опыт, происходит из ощущений, а ощущения, в свою очередь, представляют собой элементы мира.
Но В. И. Ленин разоблачил софистическую сущность всех подобных «доказательств». Ленин показал, что единственным основанием этих мнимых доказательств неидеалистической природы махизма является двусмысленность выражений: «источник познания — опыт», «ощущения — элементы мира» и т. д. Тезисы эти двусмысленны, так как в оболочке словесных выражений и предложений, имеющих обычно не идеалистический смысл, в данном случае скрывается именно идеалистическое и никакое другое понимание и мира и познания. «...Под словом «опыт»,— писал по этому поводу В. И. Ленин,— несомненно, может скрываться и материалистическая и идеалистическая линия в философии..., но ни определение опыта, как предмета исследования, ни определение его, как средства познания, ничего еще не решает в этом отношении»[46].
Ошибка, обусловленная двусмысленностью словесного выражения, может состоять и в том, что сказанное об одном предмете как члене известной совокупности однородных предметов, и в этом смысле истинное, принимается за сказанное обо всей совокупности, рассматриваемой как целое. Но совершенно очевидно, что это смешение ошибочно. Ошибка в данном случае связана с тем, что одно и то же словесное выражение может быть понято в ограничительном смысле и без ограничения.
Ошибка эта называется выводом от сказанного об отдельном, или о части целого, к сказанному о целом (fallacia a sensu distrib itivo ad sensum collectivum).Обратной формой этой ошибки является вывод от сказанного в отношении совокупности однородных предметов, рассматриваемой как целое, к сказанному об отдельном предмете этой совокупности (fallacia a sensu collectivo ad sensum distribute um).
Примером ошибочного вывода от сказанного об отдельном к сказанному о всей совокупности в целом является следующее рассуждение: так как каждая молекула воздуха, т. е. молекула азота, кислорода и т. д., движется со средней скоростью около полукилометра в секунду и так как земная атмосфера — совокупность молекул воздуха (азота, кислорода и т. д.), то, следовательно, земная атмосфера движется со скоростью около полукилометра в секунду. Вывод — явно ошибочный: хотя каждая молекула кислорода и азота, отдельно взятая, движется над землёй с указанной скоростью,— однако состоящая из этих молекул атмосфера,— если её рассматривать как целое,— не движется, но образует устойчивую воздушную сферу, облекающую земной шар.
Пример обратной ошибки в выводе. Земная атмосфера в целом удерживается притяжением Земли и не рассеивается в мировом пространстве; следовательно, и отдельные молекулы земной атмосферы удерживаются притяжением Земли и не рассеиваются в мировом пространстве. Этот вывод ошибочный. Из того, что в целом земная атмосфера, т. е. подавляющее, огромное большинство молекул атмосферы имеет скорость движения, недостаточную для того, чтобы преодолеть притяжение Земли и навсегда улететь в мировое пространство, никак не следует, будто отдельные молекулы не могут приобрести такую скорость: вследствие столкновения отдельных молекул и сложения скоростей их движения отдельные молекулы газов, составляющих воздушную оболочку земли, могут приобретать скорость, превышающую 11 километров в секунду, а следовательно, могут преодолевать притяжение Земли и навсегда покидать пределы земной атмосферы. Число таких молекул ничтожно по отношению к общему их числу в атмосфере, так что последняя в целом практически остаётся устойчивой, однако отдельные молекулы не следуют общему правилу.
Ошибка, обусловленная двусмысленностью словесного выражения, может состоять также и в соединении того, что раздельно, либо в разделении того, что соединено в самой действительности. Ошибка эта называется выводом от разделённого к составному (fallacia a sensu diviso ad sensum compositum). Обратная её форма — вывод от составного к разделённому (fallacia a sensu composito ad sensum divisum).
Примером ошибки от сказанного о разделённом к сказанному о составном может служить рассуждение тех, кто, видя, что последовательно наблюдаемые отдельные случаи размыва и выветривания гор не сглаживают сколько-нибудь заметным образом рельефа земной коры, выводят отсюда, будто и большая сумма этих случаев, накопляясь во времени, не окажет заметного сглаживающего влияния. Здесь от истинности сказанного в раздельном смысле заключают к истинности сказанного в смысле составном.
Но это — логическая ошибка. В действительности повторяющиеся в течение многих сотен тысяч и миллионов лет явления размывания и выветривания, суммируясь, совершенно стирают с лица земли даже высокие горы, «округляют» и «выглаживают» землю, порождают и неуклонно усиливают равнинный характер земных ландшафтов.
Рассмотренные выше пять видов ошибок в демонстрации были видами учетверения терминов, обусловленного двусмысленностью словесного выражения. И о та же ошибка учетверения терминов может быть обусловлена не двусмысленностью словесной формы, а ошибочным отождествлением в мысли различных по сути вещей и явлений.
К этой разновидности учетверения терминов относятся следующие ошибки.
Латинское название этой ошибки — transitus a dicto secundum quid ad dictum simpliciter. Ошибка эта — одна из распространённейших. Очень часто то, что истинно лишь при известных условиях, в ограниченном смысле, в известном отношении, используется в демонстрации доказательства как истинное безусловно, вне всяких ограничений, безотносительно. Совершенно очевидно, что для отождествления истинного лишь под известным условием с истинным безусловно нет логического основания: может быть, сказанное с известным ограничением истинно и без этого ограничения, но может быть (и часто бывает), что истинное в пределах указанного условия или отношения окажется ложным, как только его выскажут независимо от этих условий и этого отношения.
Ошибку вывода от сказанного в известном отношении к сказанному безотносительно допустил, например, Плеханов, когда он пытался разъяснить взгляд Маркса по вопросу об участии рабочей партии во временном правительстве. Маркс рассматривал этот вопрос в связи с особыми историческими условиями, которые сложились в Германии в 1850 г. Условия эти были тогда таковы, что можно было ожидать нового политического революционного взрыва и перехода власти в руки мелкобуржуазной демократической партии. В это время демократическая партия, партия мелкой буржуазии, всё более организовывалась, а рабочая партия сохранялась в организованном виде лишь в отдельных местностях и попала поэтому под руководство мелкобуржуазных демократов.
При сложившихся конкретных условиях Маркс не мог допустить даже мысли о возможности участия рабочей партии во временном правительстве. Поэтому он в «Обращении Центрального Комитета к Союзу коммунистов» совершенно не касается вопроса о допустимости участия пролетариата во временном революционном правительстве.
Разбирая это «Обращение», Плеханов сделал ошибочный вывод. Из того, что при данных конкретных политических условиях (сложившихся к 1850 г. в Германии) Маркс не считал возможным участие рабочей партии во временном революционном правительстве, Плеханов делает вывод, относящийся уже не к данным условиям, а вывод безусловный и безотносительный. Плеханов ошибочно заключал, будто Маркс «не допускал даже и мысли о том, что политические представители революционного пролетариата могут вместе с представителями мелкой буржуазии трудиться над созданием нового общественного строя»[47].
В. И. Ленин показал, что «логика этого вывода хромает»[48]. Логическая ошибка Плеханова состоит в том,что от истинного в ограниченном смысле, при определённых условиях, он заключает к истинности того же положения, но взятого уже независимо от данных условий, вообще, безотносительно. «Маркс,— пишет Ленин,— говорит только о конкретной ситуации, Плеханов делает общий вывод, не рассматривая вовсе вопроса в его конкретности»[49].
Другой пример ошибки перехода от сказанного под условием к сказанному безусловно.
Бром, принимаемый в определённой дозе, зависящей от нервной конституции высшего животного или человека, производит торможение коры больших полушарий мозга и поэтому может быть использован как ценное средство для лечения нервных болезней. Но тот же бром, принимаемый без учёта особых условий и обстоятельств нервной конституции, дозируемый стандартно, как «бром вообще», не даёт необходимого и ожидаемого результата.
Поэтому врачи, прописывающие бром безусловно, без учёта особых условий каждого данного случая, и не изменяющие соответственно этим условиям его дозировки, делают ошибку перехода от истинного под условием к истинному безусловно.
Из сказанного И. В. Сталиным в работе «Марксизм я вопросы языкознания» о начётчиках и талмудистах видно, что последние особенно легко и часто впадают в ошибку перехода от сказанного под условием к сказанному безусловно. Начётчики и талмудисты, не вникая в существо дела, цитируют чисто формально, отрывают цитаты от тех исторических условий, которые в них имеются в виду.
Так, одна из ошибок А. Холопова, обратившегося к И. В. Сталину с вопросом, может ли получиться из скрещивания языков новый язык, состояла в молчаливом предположении, будто те или иные выводы и формулы марксизма, полученные в результате изучения одного из периодов исторического развития, являются правильными для всех периодов развития и поэтому должны остаться неизменными.
Ошибка А. Холопова — типичная ошибка перехода от сказанного под условием к сказанному безусловно. Сказанное И. В. Сталиным в выступлении на XVI съезде партии о невозможности борьбы между языками в условиях и в эпоху после победы социализма во всемирном масштабе А. Холопов пытался применить — безотносительно к этим условиям — к эпохе до победы социализма в мировом масштабе, когда ещё не ликвидирован империализм. В результате А. Холопов запутался в мнимом, им самим вымышленном противоречии. Причина этого противоречия — в попытке выводить от сказанного применительно к известным условиям к сказанному безотносительно и безусловно.
Ошибка эта тесно примыкает к предыдущей. Она состоит в том, что случайный признак предмета или явления принимается в качестве существенного, необходимого и поэтому всегда присущего данному предмету или явлению.
В результате отождествления случайного признака с признаком существенным положение, истинное только относительно некоторых предметов класса, ошибочно утверждается как истинное относительно любого предмета класса. Ошибка эта называется ошибочным выводом «от случайного» (fallacia accidentis).
Ошибочный вывод от случайного часто встречается в индуктивных обобщениях. Заметив, что известное свойство обнаружено во всех наблюдавшихся до сих пор предметах класса, неосторожные исследователи часто думают, будто свойство это — существенное для предметов данного класса и потому должно быть обнаружено не только в уже рассмотренных экземплярах, но и во всяком представителе того же класса.
Совершенно очевидно, что для такого заключения нет логического основания. Свойство, обнаруженное в нескольких (и даже многих) предметах класса, может оказаться существенным, но может оказаться и случайным. В последнем случае наличие свойства в рассмотренных представителях класса ничего ещё не говорит о том, имеется ли это свойство налицо и в остальных предметах класса.
Так, К. А. Тимирязев вскрыл ошибочность распространённого среди биологов взгляда, будто всякое скрещивание между видами имеет результатом бесплодие. Обобщение это основывалось на наблюдении, что мулы и лошаки, т. е. помесь лошади посла,— бесплодны. Следствие скрещивания лошади и осла — бесплодие помеси — было распространено на всякое скрещивание между видами. Таким образом, результат, не существенный для решения вопроса в общем виде и в этом смысле — случайный, был безосновательно истолкован как существенный и возведён в общее правило. К. А. Тимирязев показал на ряде примеров из жизни растений и животных, что скрещивание некоторых видов «бывает не только не бесплодно, но даже плодовитее, чем самооплодотворение»[50].
Ошибка учетверения терминов, обусловленная отождествлением в мысли различного, часто выступает в демонстрации в форме ошибочного вывода о причине. В этом случае ошибка состоит в том, что обстоятельство или факт, которые не являются причиной данного явления, ошибочно принимаются за причину (fallacia поп causae ut causae).
Одним из наиболее распространённых поводов для ошибки ложного вывода о причине является смешение последовательности фактов во времени с причинной связью тех же фактов. Если часто наблюдалось, что за фактом а следует факт 6, то в уме, логически недисциплинированном, легко может возникнуть мысль, будто предшествующий во времени факт есть причина, а следующий за ним — действие этой причины. Но для такого вывода нет достаточного основания. Предшествующий факт может быть действительно причиной последующего, но он может быть и просто предшествующим фактом, не стоящим ни в какой причинной связи с тем, который за ним следует. Чтобы решить вопрос, будет ли предшествующий факт причиной, необходимо особое исследование, опирающееся не только на последовательность двух фактов во времени и не только на частую повторяемость этой последовательности.
Если ошибочный вывод о причине принимает форму вывода, основывающегося на одной лишь последовательности фактов или событий, то такой вывод характеризуется формулой: post hoc ergo propter hoc («после этого, следовательно, по причине этого»). Даже самые простые факты показывают несостоятельность подобного рода выводов. Из того, например, что весной скворцы прилетают позже грачей (и это повторяется из года в год) вовсе не следует, что прилёт грачей является причиной прилёта скворцов.
Простая последовательность фактов или событий во времени сама по себе не доказывает необходимой причинной связи между ними. Чтобы доказать, что предшествующий факт — причина, а следующий за ним — действие этой причины, необходимо нечто большее, чем простое наблюдение последовательности, — необходима проверка догадки о причине практикой, экспериментом. «...Доказательство необходимости,— говорит Энгельс,— заключается в человеческой деятельности, в эксперименте, в труде: если я могу сделать некоторое post hoc, то оно становится тожественным с propler hoc»[51].
Кроме ошибок «чересчур поспешного вывода» и «учетверения терминов» со всеми их разновидностями, в демонстрации встречается ещё ошибка, обусловленная неправильным пониманием логической связи между основаниями и заключением.
Ошибка эта — ошибка ложного следования (fallacia conseq ientis) — встречается в условных умозаключениях. Как известно, в умозаключениях этих: 1) из истинности основания необходимо вытекает истинность следствия; 2) из ложности следствия необходимо вытекает ложность основания. В то же время 3) при ложности основания вопрос об истинности или ложности следствия остаётся открытым: в одних случаях следствие будет ложным, в других — истинным. И точно так же 4) при истинности следствия вопрос об истинности или ложности основания остаётся открытым: в одних случаях основание будет истинным, в других — ложным.
Правила эти нередко нарушаются как в отдельных умозаключениях, так и в умозаключениях, входящих в демонстрацию доказательства. При этом, как легко убедиться, ошибки встречаются не в умозаключениях от истинности основания и не в умозаключениях от ложности следствия. Никому обычно не приходит в голову заключать от истинности основания к ложности следствия или от ложности следствия к истинности основания.
Напротив, в умозаключениях от ложности основания и от истинности следствия нередко возникают ошибки. А именно: нередко от ложности основания заключают к необходимой ложности следствия, что, конечно, неверно, так как в этом случае следствие может оказаться не только ложным, но и истинным. И точно так же нередко от истинности следствия заключают к необходимой истинности основания, что тоже неверно: при истинности следствия основание может быть в одних случаях истинным, в других — ложным.
Так, известно, что если происходит солнечное затмение, то в это время всегда — новолуние. Однако было бы ошибкой заключить отсюда, что если в данный момент затмение не наблюдается, то не может быть и новолуния. Ложность основания не означает необходимой ложности следствия: возможно, что затмения нет, но в то же время имеет место новолуние. И точно так же было бы ошибкой заключить, что если в данный момент новолуние, то в этот же момент всегда должно наблюдаться и затмение. Так как истинность следствия не означает необходимой истинности основания, то при истинности следствия основание может быть и ложным: при новолунии затмения может не быть (в большинстве случаев именно так и бывает).
Не всякое условное умозаключение отражает связь между причиной и действием.
В тех условных умозаключениях, которые отражают эту связь, одной из возможных причин ошибки ложного следования бывает незнание или забвение того, что одно и то же действие может быть вызвано не только одной единственной, но в иных случаях и несколькими причинами. Если бы действие вызывалось всегда одной единственной причиной, то в отсутствии причины мы с полным нравом могли бы видеть основание для отрицания её действия, а в наличии действия — такое же основание для утверждения наличия его причины. Так, если врачу известно, что только дифтерия даёт при исследовании слизистой оболочки зёва бациллы Лёфлера, то врач имеет все основания при наличии этих бацилл в слизистой оболочке зёва больного заключить, что у больного — дифтерия. И точно так же при отсутствии бацилл Лёфлера в слизистой оболочке зёва врач имеет все основания заключить, что данное заболевание — не дифтерия.
Напротив, если врачу известно, что данный симптом — например боль в горле — наблюдается не при одной единственной болезни, а при нескольких, например при гриппе, ангине, дифтерии, скарлатине и т. д., то одно лишь наличие боли в горле не даёт основания, необходимого для заключения о том, чем именно заболел человек. Здесь вероятны несколько причин, и для установления действующей в данном случае причины требуется дополнительное исследование, рассмотрение всех других симптомов заболевания и т. д.
Так как некоторые действия вызываются каждое одной единственной причиной, другие же — несколькими, то в условных умозаключениях, отражающих причинные связи явлений, легко может возникнуть ошибка, состоящая в заключении от ложности основания или в заключении от истинности следствия. Ошибка эта обусловлена тем, что неоднозначное отношение между основанием и следствием принимается за однозначное.
Для избежания этой ошибки необходимо помнить, что логических примет однозначности связи между основанием и следствием не существует. До тех пор, пока мы опираемая только на логические правила и не знаем, какова в данном случае обусловленность действия причиной, умозаключение должно строго подчиняться всем ограничениям логических правил условных выводов. Согласно этим правилам необходимым будет только заключение от истинности основания к истинности следствия и от ложности следствия к ложности основания. Напротив, заключения от ложности основания и от истинности следствия — всегда проблематичны: они могут оказаться как истинными, так и ложными.
Уточнение связи основания со следствием в этом последнем случае даётся не логикой, а фактическим исследованием вопроса. Только такое исследование может дать нам знание о том, какими и сколькими причинами может вызываться данное действие. Исследование это — задача специальных наук, вооружённых аппаратом логического мышления, вооружённых марксистским диалектическим методом исследования, но не задача логики.